Beyond 0.05: Interpreting P-Values in a Clinical Trial

Frequentist Thinking III − Beyond 0.05: Interpreting P-Values in a Clinical Trial
Keywords: clinical trial, p-value, research hypothesis, survival & competing risks
正しくp値を解釈するための考え方
私「ただいま、お父さん。そろそろダウン出さなきゃだめだね。あ、ホットコーヒーもらっていい?」
お父さん「そろそろ帰る時間だと思って、たっぷり淹れてた。そうそう、JCOG9502の論文で生存曲線とp値の話をしたことがあったよね(Sasako, et al. 2006)。そのとき気になったんだけどさ。どうしてp値が0.05より小さいと統計学的に有意っていったの?」
私「それがルールなんじゃないの?」
お父さん「そこはね、論文の読み方を間違えてる。質問していい?論文に目を通すとき、最初にAbstract(抄録)を読むでしょ。次にどこを読む?」
私「Results(結果)。だってどういう結果だったかはやく知りたいもん」
お父さん「うんうん、その気持ちはすごくわかる。でも、p値を見るときに限っては、正しく解釈するために、事前にMethods(方法)を読んでおく必要がある。科学コミュニティのなかで、p値について誤解が多いことが問題視されていて、アメリカ統計協会(ASA)が、統計を専門としない研究者、実務家、サイエンスライター向けの声明を出したことがある。そのきっかけは、2014年2月のASAフォーラムにこんな投稿がなされたことだった」
私「なんだこの禅問答」
Q. Why do so many colleges and grad schools teach p ≤ 0.05?(なぜ多くの大学、大学院で「p ≤ 0.05」と教えているのか?)
A. Because that’s what the scientific community and journal editors use(なぜなら科学コミュニティと雑誌編集者が依然として0.05を使っているからである)
Q. Why do so many people still use p ≤ 0.05?(なぜ多くの人々が「p ≤ 0.05」を依然として使うのか?)
A. Because that’s what they were taught in college or grad school(なぜなら彼らが大学、大学院でそう教わったからである)
お父さん「そして、ASAはp値の使い方について6つの原則を出した」
- p値はデータと特定の統計モデル(訳注:仮説も統計モデルの要素の1つ)が矛盾する程度を示す指標の1つである
- p値は、調べている仮説が正しい確率や、データが偶然のみで得られた確率を測るものではない
- 科学的な結論や、ビジネス、政策における決定は、p値がある値(訳注:有意水準)を超えたかどうかにもとづくべきではない
- 適正な推測のためには、すべてを報告する透明性が必要である
- p値や統計的有意性は、効果の大きさや結果の重要性を意味しない
- p値は、それだけでは統計モデルや仮説に関するエビデンスの、よい指標とはならない
私「さっきのやり取りがきっかけで、学会でp値批判があったってわけね。でもまあ6つとも抽象的でぴんとこないな」
お父さん「そう?“科学的な結論は、有意水準を超えたかどうかにもとづくべきではない”なんてのは、かなり明確に書いてあると思うけど。JCOG9502論文でいえば、原則3や原則5は、p値だけ見るんじゃなくて、生存曲線をじっくり観察してから結論を出そうっていってるんだ。もちろん専門知識がないと、原則がなにを意図しているかはわかりにくい。原則4は、たとえば多重性の問題(multiplicity)に関係している」
私「多重性?」
お父さん「最近の臨床試験では、多重性っていう統計的な問題が潜んでいることが多い。JCOG9502論文を例にもう少し説明しようか。Statistical Analysis(統計解析)のところを読み返してみて。alpha error(αエラー)っていうのは、有意水準ともいうけど、どちらもp値と比べる水準のこと」
After 8 years of slow accrual, the JCOG data and safety monitoring committee approved an amendment to the sample size and analysis plan. The amended sample size was 250, with one-sided alpha error of 0.1 and beta error of 0.2, with a 12-year accrual period (in total) and 8-year follow-up.(JCOG9502論文[Sasako, et al. 2006]の”Statistical Analysis”から抜粋)
私「p値を0.1と比べるってこと?0.05じゃないの?」
お父さん「うん、αエラーの理想は教科書通りの0.05。試験途中にαエラーは変えるべきではない。そんなことはみんなわかってるんだ。でも、現実に登録が難航すると、軌道修正が必要になることもある。この試験もそう。苦肉の策でαエラーを0.1に緩めたみたい」
私「読み飛ばしてた。自由すぎるなJCOG」
お父さん「あとさ、ASA声明の原則4とその解説を念頭に置いて、JCOG9502の図Aと図Bを見てみてよ。生存曲線が2本、p値が4つ示されているよね。この複数のp値は、どう読み解けばいいかわかる?」
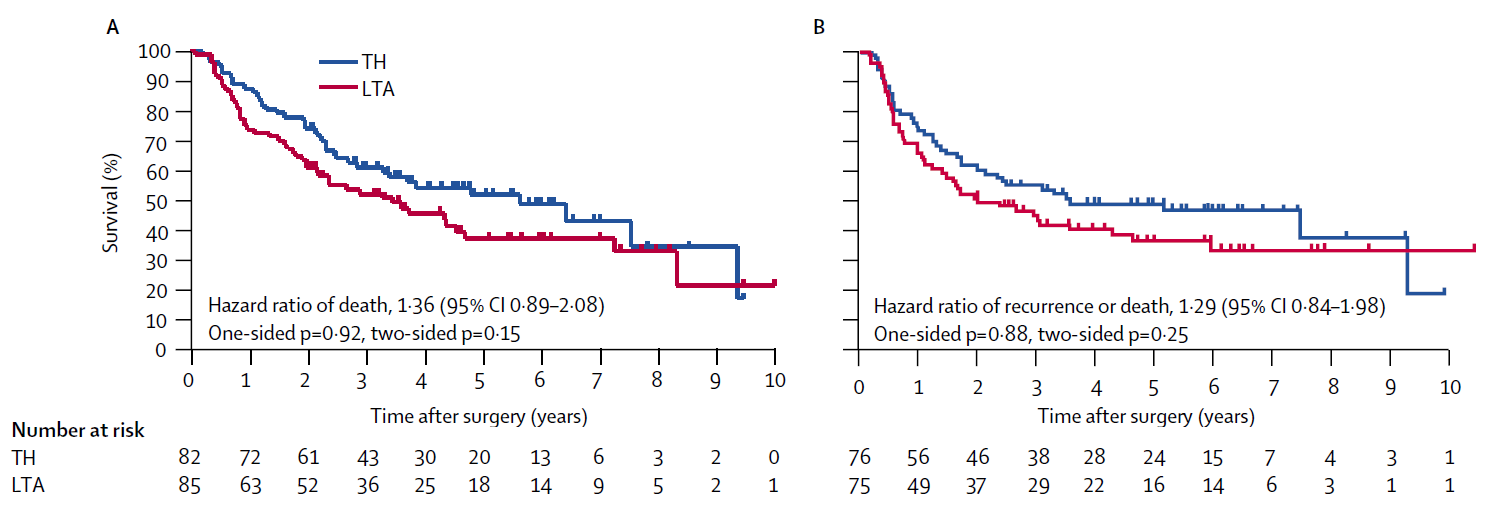
私「もともとそれが知りたくて、お父さんに質問したんだけど、わかってる?図Aのp値と図Bのp値については、私もちゃんと考えてたよ。図Aの方を見ればいいんでしょ。JCOG9502の主要エンドポイントはOSで、図Aが全生存曲線だもの。でも図Aだけでも片側と両側があるじゃない。ここが意味不明で、考えこんじゃった」
お父さん「それはそんなに難しくない。臨床試験で、試験治療群と標準治療群の成績を比べるとするでしょ。試験治療群が勝ったときだけ、有意差があったって宣言するのが、片側p値。どちらの群が勝っていても、統計的に有意かどうか判定するのが、両側p値だよ」
私「論文を読むと、JCOG9502のプロトコール上、LTAが試験治療、THが標準治療とされてたんだよな。LTAの方が、侵襲性が高いからかな。だからLTA群の予後がいいっていう結果でないと、有意差ありって宣言しないわけだ。これって普通?」
お父さん「いや?両側p値を使うのが普通。でもJCOGが行っている臨床試験では、試験治療群の成績が、標準治療群よりいいかどうかに興味があり、しかも毒性や侵襲の異なる治療同士を比べることが多いので、片側仮説の方が自然なんだ。そのためこのグループでは、片側p値の採用を許容している(Japan Clinical Oncology Group 2025)。片側p値で有意じゃなかったら、標準治療を使い続けるから、それでいいんだって。この論文の両側p値は参考値みたいだね。つまり、有効性の主たる判断には、図Aの片側p値だけが用いられることになる」
私「ストーマ造設あり・なしと復職状況を調べる私の調査だったら、仮説の意味から考えても両側p値がおすすめってことね。よく分かりました」
あらゆる科学論文でp値が用いられていますが、p値が誤用されたり、研究結果の解釈に悪い影響を与えたりする弊害が指摘されています。典型的なものを挙げると、研究で小さいp値が得られると、それだけで重要な知見が得られたとみなされたり、機械的にp値が0.05より小さいというだけで意思決定がなされたりするケースは、皆さんもよく目にするのではないでしょうか。
ASAは2016年に、定量的研究の実施とその解釈を改善するため、p値の適正な使用と解釈に関する6つの原則をまとめました(Wasserstein and Lazar 2016)。以下に引用します。
- p値はデータと特定の統計モデル(訳注:仮説も統計モデルの要素の1つ)が矛盾する程度を示す指標の1つである
- p値は、調べている仮説が正しい確率や、データが偶然のみで得られた確率を測るものではない
- 科学的な結論や、ビジネス、政策における決定は、p値がある値(訳注:有意水準)を超えたかどうかにもとづくべきではない
- 適正な推測のためには、すべてを報告する透明性が必要である
- p値や統計的有意性は、効果の大きさや結果の重要性を意味しない
- p値は、それだけでは統計モデルや仮説に関するエビデンスの、よい指標とはならない
統計学の教科書では、p値と帰無仮説の関係を中心に説明しています。しかしp値を解釈するとき大切なのは、帰無仮説だけではありません。ASA声明の趣旨は、研究計画やデータの収集から結果の報告に至るまで、統計解析の背景にあるあらゆる情報を利用しなければ、p値は正しく解釈できないということです。
原則4に注目してみましょう。ASA声明では、原則4の解説として「複数のデータ解析を実施して、そのうち特定のp値のみを報告することは、報告されたp値を根本的に解釈不能としてしまう」と述べています。かみ砕いて言うと、たくさんp値があると、そのなかで都合のいいp値を採用してしまいますよね。このような、いいとこどりの解析は、科学者の間で意識的にも無意識にも広く行われていて、偽陽性(false positive)の研究結果 ばかりが報告される一因ではないか、という問題意識を統計学者はもっています。この問題は、統計学で多重性(multiplicity)や選択的推論(selective inference)と呼ばれています。
p値と仮説検定(hypothesis test)は、研究仮説が正しいかどうかについて、二者択一の判断をするための統計手法です。なんだか難しそうなので、例え話で説明しましょう。
コイン投げをして、6回連続で表が出たとします。このコインは、イカサマコイン(表が出る確率が1/2でない)でしょうか?p値では以下のように考えます。表が出る確率は1/2という仮説の下で、6回連続で表の確率は(1/2)の6乗で0.0156ですよね。6回連続で裏の確率は同じく0.0156です。すなわち、このような極端なデータが得られる確率は、足してp=0.0312と極めて低いことがわかります。このような極端なデータが得られるのはおかしくはありませんか?従って、このコインにはイカサマがある、というのが、p値を用いて仮説(表が出る確率は1/2)を否定するときのロジックです。
片側(one-sided)p値と両側(two-sided)p値は、コインの片側(表だけ)をみるか、両側(表と裏)をみるかに、それぞれ対応しています。コイン投げの例え話でいえば、片側p値はp=0.0156、両側p値はp=0.0312です。
JCOG9502に戻って考えてみましょう。仮説検定では3段階の手続きを行います。まず、仮説を設定します。JCOG9502では、真実は「LTA群はTH群に比べ全生存期間を延長する効果がある」と「効果がない」の2通りがあり得ます。仮説検定では、「効果がない」という仮説に注目して、帰無仮説(null hypothesis)と呼びます(こちらが、表が出る確率が1/2に対応します)。
次に、帰無仮説の下でデータがどのように分布するかを調べます。仮に、同じ対象者167人の試験を1000回繰り返したと想像してみてください。これが頻度論の思考様式です。仮に効果がなかったとしても、ランダム誤差のため、LTA群の生存曲線の方がよい場合もあれば、TH群の方がよい場合もあるでしょう。しかし1000回繰り返した結果は、差がないという結果を中心に分布するはずです。そこで、この1000回の分布と、実際に観察されたデータとを比べp値を計算します。
p値とは、帰無仮説が正しい、つまり生存曲線に差がない、という仮定の下で、実際に観察された2本の生存曲線の差よりも、極端な差が観察される確率のことです。もしp値が小さければ、こんなに確率の低いことが起きるわけがない、だから生存曲線に差がないというそもそもの前提条件が間違いだ、という判断になるわけです。逆に、p値が大きければ、当たり前のことが起きたという意味になります。
非劣性試験や同等性試験を除くほとんどのランダム化臨床試験で、両側p値が標準とされている理由として正しいものは、次のうちどれでしょうか。
- 試験治療が優れていたとしても、劣っていたとしても、差があるなら結論を出したいから
- 統計学者の間の決まりごと
- 世界中の臨床試験で統一した方が、混乱が少ないから
- ランダム誤差は、平均の上方向と下方向の両方のばらつきを生じるから
- 正解は3です
これは歴史的経緯によるものです。1998年にICH E9ガイドラインが策定されたとき、米国、欧州、日本の規制当局で、両側p値を基本にすることが合意されました(吉村2003)。
文献
JCOGプロトコールマニュアル version 3.8 [Internet]. 東京: Japan Clinical Oncology Group; 2025
Sasako M, Sano T, Yamamoto S, Sairenji M, Arai K, Kinoshita T, Nashimoto A, Hiratsuka M, Japan Clinical Oncology Group (JCOG9502). Left thoracoabdominal approach versus abdominal-transhiatal approach for gastric cancer of the cardia or subcardia: a randomised controlled trial. Lancet Oncol 2006;7(8):644-51
Wasserstein R and Lazar NI. The ASA’s statement on p-values: Context, process, and purpose. Am Statistician 2016; 70: 129-33(日本語訳)
吉村功. 検証的臨床試験における有意水準と試験の数-「臨床試験のための統計的原則」との関連で-. 計量生物学 2003; 24: S3-9