From Risk and Rate to Survival and Hazard

「生存曲線やハザード比について納得感が足りないの」生存時間解析の基礎を整理するcoffee-chat guide。時間を含む効果理解への入り口です。
Published

December 13, 2025

Effects and Time V − From Risk and Rate to Survival and Hazard

Keywords: effect measure, probability model, R simulation, survival & competing-risks

リスクと時間の関係

私「お父さんさ、以前聞いた寄与割合の話を思い返して気づいたんだけどね。まだ納得感が足りないの」

お父さん「なに？コーヒーと一緒にこういう話をするのは歓迎だよ」

私「がん検診後、10年、12年、20年って見ていくと、寄与割合が変わるって話だったでしょ。リスクには時間の概念があるって。あれって、2値データじゃなくて生存時間データになってない？ていうか、あれは生存曲線か」

お父さん「そうだよ。リスクと生存曲線は表裏一体なんだ」

私「生存曲線からある時点の生存確率を読み取ると、1-リスクになっているっていう意味ね。うんうん。そして、疫学の教科書に出てくる率（rate）が、生存時間解析のハザード（hazard）に対応しているっていうのもわかる。でも、気になるのはハザード比（hazard ratio）なんだ。寄与割合とかリスク比とかって、時間とともに変化するっていうけど、ハザード比は変化しないんだっけ」

お父さん「変化しない。正確にいうと、生存曲線をみると変化している状況もあり得るんだけど、時間を通じてハザード比は一定と、無理やり仮定して計算してる」

私「リスク比は変化するけどハザード比は変化しないの？矛盾してない？」

お父さん「えーっと、リスク比が変化しないわけじゃなくて…。リスクはハザードの時間積分だから、どちらか一方の比を固定したらもう一方は固定できなくて…。ちょっと紙ナプキンとペンをとってくれる？教科書通りに説明するとこうなるんだけど。まずはリスクとハザードからはじめるね」

生存曲線とハザードの関係

これまでのエピソードでは、ある時点までのリスクを扱ってきましたが、今度は“時間に沿って変化するリスク”を推定したKaplan-Meier曲線について正式に説明します。Kaplan-Meier曲線は、そもそも2値データではなく生存時間データに用いられる手法でした。そのため、Kaplan-Meier曲線は時間軸を横にとったグラフですし、いわゆるハザード比との関係も知りたいところですよね。ここでは、ハザードが時間を通じて一定という単純な状況で、そのあたりを整理しましょう。

Kaplan-Meier曲線は、生存時間データから計算された推定値を、時間軸（\(x\)軸）に沿ってグラフにしたものです。これを数式で書くなら、「生存曲線を時間\(x\)の関数\(S(x)\)で表す」ということになります。

関数\(S(x)\)を具体的に書くこともできます。生存時間が、ハザードが時間を通じて一定ということは、指数分布に従うと仮定したことになります（これはKaplan-Meier曲線とは別ものです）。指数分布の形状を決めるパラメータ（ハザード）は、\(λ\)という記号で表すことが普通です。このとき指数分布の生存関数とハザードには、以下のような関係があります。

\(S(x)=\mathrm{exp}(-\lambda x)\)

ここまでくればあと一息です。最後に、疾患リスクとハザードの関係を確認しましょう。疾患リスク\(π\)は、特定時点\(x\)までに疾患を発症する確率を表しています。つまり、疾患リスク\(π\)とハザード\(λ\)は、時点\(x\)の生存関数を\(S(x)\)を介して、以下の式で結びついています。

\(\pi=1-S(x)=1-\mathrm{exp}(-\lambda x)\)

私「わからん。数式はわからん」

お父さん「そう？数学の難しさというより、この等式が何と何を結びつけているかが、慣れないと読み取りにくいんだと思う。ちょっとしたポイントは指数分布だとハザードは定数扱いで、生存関数は時間の関数だってところかなあ」

私「結びつきねえ。とりあえず生存曲線とハザードの関係式ってことまでかな、確実なのは」

お父さん「まずはそこからだね。多分、指数分布からデータを発生させるシミュレーションをやってみると、この式とデータの関係が見えてくると思う」

generate_data <- function(n=200, hr1, hr2) {
  stoma <- rbinom(n, size = 1, prob = 0.4)
  sex <- rbinom(n, size = 1, prob = 0.5)
  age <- rnorm(n, mean = 65 + 3 * stoma, sd = 8)
  hazard_relapse   <- ifelse(stoma == 1, hr1*0.10, 0.10) # 再発のハザード（大きいほど早く起こる）
  hazard_death     <- ifelse(stoma == 1, hr2*0.10, 0.10) # 死亡のハザード（大きいほど早く起こる）
  hazard_censoring <- 0.05                               # 打ち切りハザード（群に依存しない）
  
  t_relapse   <- rexp(n, rate = hazard_relapse)   # 再発までの潜在時間
  t_death     <- rexp(n, rate = hazard_death)     # 死亡までの潜在時間
  t_censoring <- rexp(n, rate = hazard_censoring) # 打ち切りまでの潜在時間
  
  ## --- 全生存期間（OS） ----------------------------------------
  time_os   <- pmin(t_death, t_censoring)
  status_os <- as.integer(t_death <= t_censoring)  # 1 = 死亡, 0 = 打ち切り
  
  ## --- 無再発生存期間（RFS） -----------------------------------
  time_rfs <- pmin(t_relapse, t_death, t_censoring)
  
  status_rfs <- integer(n)
  status_rfs[time_rfs == t_relapse & time_rfs < t_censoring] <- 1 # 再発
  status_rfs[time_rfs == t_death & time_rfs < t_censoring] <- 1   # 死亡
  
  ## --- 累積再発率（CIR） + 競合リスク --------------------------
  time_cir <- pmin(t_relapse, t_death, t_censoring)
  
  status_cir <- integer(n)
  status_cir[time_cir == t_relapse & time_cir < t_censoring] <- 1 # イベント1: 再発
  status_cir[time_cir == t_death & time_cir < t_censoring] <- 2   # イベント2: 競合リスクとしての死亡
  
  ## --- データフレームにまとめる --------------------------------
  dat <- data.frame(
    id         = 1:n,
    sex        = factor(sex, levels = c(0, 1), labels = c("WOMAN", "MAN")),
    age        = age,
    stoma      = factor(stoma, levels = c(0, 1),
                        labels = c("WITHOUT STOMA", "WITH STOMA")),
    time_os    = time_os,
    status_os  = status_os,
    time_rfs   = time_rfs,
    status_rfs = status_rfs,
    time_cir   = time_cir,
    status_cir = status_cir
  )
}
cifplot()によるKaplan-Meier曲線

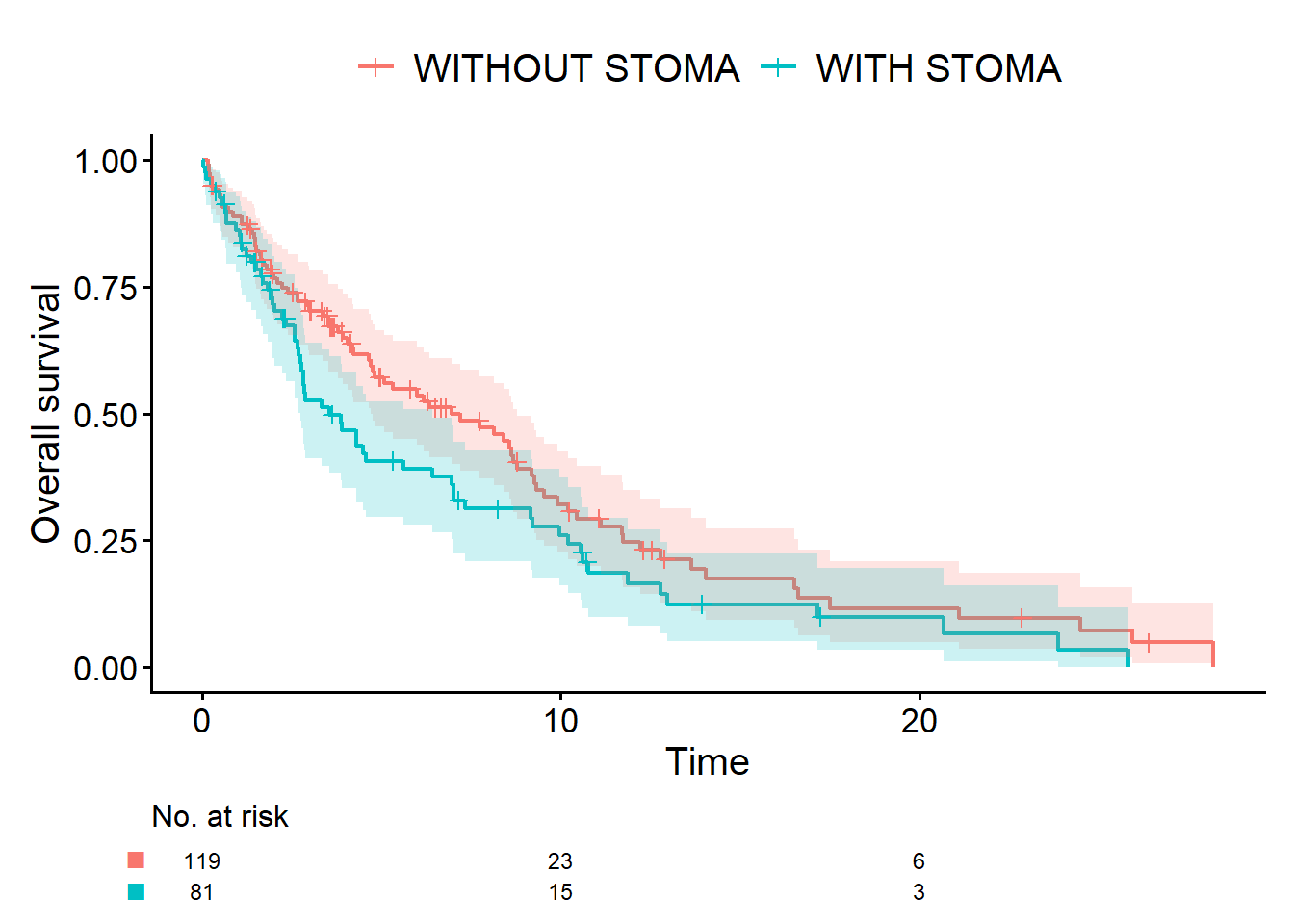
どのようなシミュレーションデータが得られるかイメージしやすいように、cifplot()で描いたKaplan–Meier曲線とcoxph()の結果を置いておきます。

# devtools::install_github("gestimation/cifmodeling") #インストールが必要なら実行 
library(cifmodeling)
set.seed(46)
dat <- generate_data(hr1=2, hr2=1.5) #再発ハザード比2, 死亡ハザード比1.5のデータ生成
cifplot(Event(time_os, status_os) ~ stoma,
  data         = dat,
  outcome.type = "survival",
  label.y      = "Overall survival"
)

# install.packages("survival") #インストールが必要なら実行
library(survival)
fit <- coxph(Surv(time_os, status_os) ~ stoma, data = dat)
summary(fit)
Call:
coxph(formula = Surv(time_os, status_os) ~ stoma, data = dat)

  n= 200, number of events= 144 

                  coef exp(coef) se(coef)     z Pr(>|z|)  
stomaWITH STOMA 0.3199    1.3769   0.1693 1.889   0.0589 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

                exp(coef) exp(-coef) lower .95 upper .95
stomaWITH STOMA     1.377     0.7262    0.9881     1.919

Concordance= 0.544  (se = 0.024 )
Likelihood ratio test= 3.51  on 1 df,   p=0.06
Wald test            = 3.57  on 1 df,   p=0.06
Score (logrank) test = 3.6  on 1 df,   p=0.06

私「ふむふむ。ハザードで指数分布を指定すると生存曲線が決まるわけね」

お父さん「そういうこと。次に気になるはハザードだよね。このパラメータの具体的なイメージを持つのは難しいけど、生存時間中央値と結びつけるのがよくやる手だよ。中央値（median）は生存曲線がちょうど50%まで落ちる時点のこと」

ハザードと生存時間中央値の関係

さて、ハザードは生存曲線が下がるスピードを決める数値です。生存時間がどのくらいの長さなのかは、中央値で測ることができます。生存時間中央値\(M\)は、生存確率50%つまり\(S(x)=0.5\)になるような時間\(x\)のことです。つまり、指数分布では

\(0.5=\mathrm{exp}(-\lambda M)\)

と関係が成り立つので、生存時間中央値\(M\)は、ハザード\(λ\)から以下のように計算することができます。

\(M = \frac{\log 2}{\lambda} \approx \frac{0.7}{\lambda}\)

私「あ、これはちょっとわかった気がする。寿命（生存時間中央値）とハザードが逆数の関係ってことね。つまり寿命が2倍になったらハザードは1/2になる」

お父さん「そうだね、たとえるならハザードはコーヒーにとっての気温みたいなもの。寒いとコーヒーが覚める時間が短くなる。これがハザードが高いってこと。正確に逆数になるのは、指数分布の下で計算するときだけどね。ハザード比は、まさにハザードの比をとったものだよ。指数分布ではこういう式になる。2つの集団の生存曲線を比較するときによく使うよね」

  • 指数分布のハザード比 \[ HR=\frac{\lambda_1}{\lambda_2} \]
このエピソードに関係するクイズです

生存時間中央値を報告してよいのは、どのような場合でしょうか？

  1. 目安としてサンプルサイズが100人以上のとき
  2. すべての対象者が予定された追跡期間を終了したとき
  3. 半数以上の対象者がイベントを起こしたとき
  4. 1、2、3すべて誤り
  • 正解は3です

生存時間データでは一部の対象者で打ち切りがあること（これ以上生存時間が長いことしかわからない）、中央値（median）の定義を思い出してください。半数以上の対象者がイベントを起こし、生存時間が確定しないと、生存確率は50%以下になりません。

次のエピソードとRスクリプト