After Cox Regression: A Case Study and R Demonstration

Effects and Time VI − After Cox Regression: A Case Study and R Demonstration

Keywords: bias, effect measure, R simulation, survival & competing risks

ハザード比が意味を持つとき、持たないとき

お父さん「もう一杯コーヒーをもらっていい？」

私「私も欲しい」

お父さん「うん、ゆっくり考えよう、大事なところだ。比例ハザード性はCox回帰の特徴そのもので、これさえ満たされれば、Cox回帰は幅広いデータにも使えるんだけど、たまに比例ハザード性が崩れたデータをみることがある。これはオンコロジー領域では必須知識かもしれない。このKaplan-Meier曲線をみてよ（Mok, et al, 2009）。生存曲線がクロスした有名なケースなんだ」

私「あ、よかった。数式ばかりで眠くなりかけてた」

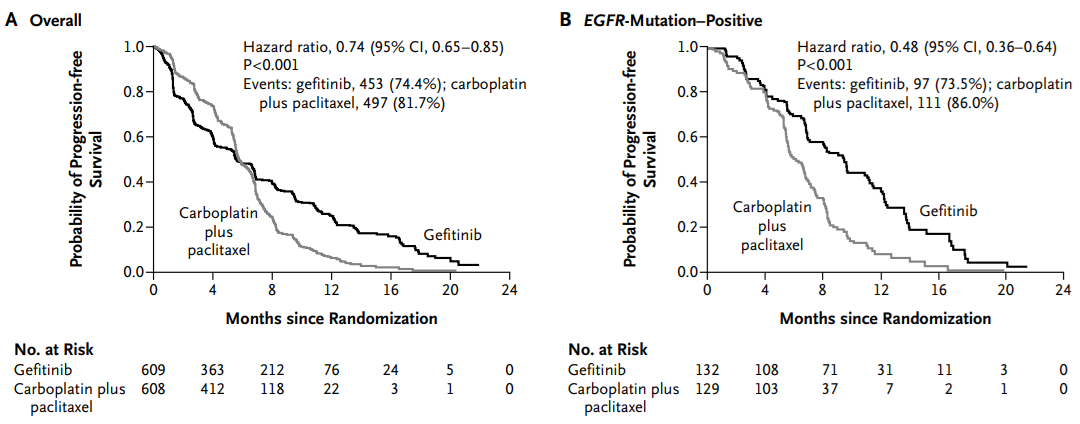
お父さん「これはステージIIIB～IVの肺がん患者の臨床試験で、ゲフィチニブと化学療法を比較している。図Aでは6ヶ月まではゲフィチニブ群の無増悪生存確率が低く、それ以降は高くなっているでしょ。こういうときは比例ハザード性が成り立っていないから、ハザード比に意味はない」

私「どうしてこうなっちゃったの？」

お父さん「それはゲフィチニブがEGFR変異陽性の肺がん患者に特に有効だったからだといわれている。図Bは、EGFR変異陽性だった261人を対象にしたKaplan-Meier曲線なんだけど、生存曲線はクロスせず、最初から最後までゲフィチニブ群の方が化学療法群より予後がいいでしょ」

私「そうだね。この試験のKaplan-Meier曲線では、治療成績が交差して、どっちが効くのか悩ましいってことはわかるよ、数式はともかくとして」

お父さん「はっきりいうとね、ハザードやハザード比が直感的にわかる人の方が少ないよ。だから安心していい」

私「え、そうなの？なんか“知らないといけない基本”みたいに思って焦った」

お父さん「ハザードはね、患者さんの健康状態を表す“見えない時計”だと思うといい」

私「見えない時計？」

お父さん「治療Aを受けた患者は、ちょっと速く進む時計を持っている。治療Bの人は、少し遅い時計を持っている。ハザード比は、2つの時計が“どれくらい違う速さで動くか”の比なんだ」

私「なるほど、時間が進むスピードの違いなら、イメージしやすいかも」

お父さん「ただし、ここが重要。時計の進み方は、必ずしも一定とは限らない。最初は治療Bが有利でも、途中から追いつかれることだってある」

私「それ、診療していてもあるかも」

お父さん「まとめると、このたとえ話の主張はこんなこと。

ハザード比は、2つの時計が“どれくらい違う速さで動くか”の比に例えられる。 比例ハザード性が成り立たないと、最初は一方の治療が有利でも、途中から追いつかれることもある

それなのに多くの論文で“ハザード比＝一定”という前提で解析する。Cox回帰が標準的に使われるからね。だから、比例ハザード性が破綻すると、ハザード比の解釈が急に怪しくなる」

私「んなこといっても、論文にはだいたいハザード比しか書いてないよね」

お父さん「だから次の一手が必要になる。“ある時点のリスク”や”ある時点までの生存曲線”を比べるんだ。曲線が交差していたら、5年生存率とか10年死亡率のようにどこを比較するか決める。ハザード比も重要だから、それとあわせてね」

シミュレーションデータにおける時点ごとのリスク比の推定

さっきの「見えない時計」をデータで眺めてみましょう。以前と同じ、ストーマ造設の有無で死亡のハザードが異なる生存時間データをシミュレーションし、時点ごとのリスク比（RR） を推定してみます。ハザード比は「時計の速さの比」でしたが、「術後10年時点の死亡リスクは、ストーマあり群が何倍か」のようにリスク比の方が、解釈しやすいこともあります。Cox回帰では時点を通じて1つのハザード比を仮定するのに対して、cifmodelingパッケージのpolyreg()では、時点を通じて一定のリスク比だけでなく、任意の時点ごとのリスク比も推定できます。

先ほどのシミュレーションデータを使って、time.pointを変えたpolyreg()を当てはめることで、術後5年・10年・20年時点の死亡リスク比を推定します。アウトカム（OS）はEvent(time_os,status_os)、曝露変数であるストーマの有無はexposure="stoma"で指定しています。

generate_data <- function(n=200, hr1, hr2) {
  stoma <- rbinom(n, size = 1, prob = 0.4)
  sex <- rbinom(n, size = 1, prob = 0.5)
  age <- rnorm(n, mean = 65 + 3 * stoma, sd = 8)
  hazard_relapse   <- ifelse(stoma == 1, hr1*0.10, 0.10) # 再発のハザード（大きいほど早く起こる）
  hazard_death     <- ifelse(stoma == 1, hr2*0.10, 0.10) # 死亡のハザード（大きいほど早く起こる）
  hazard_censoring <- 0.05                               # 打ち切りハザード（群に依存しない）
  
  t_relapse   <- rexp(n, rate = hazard_relapse)   # 再発までの潜在時間
  t_death     <- rexp(n, rate = hazard_death)     # 死亡までの潜在時間
  t_censoring <- rexp(n, rate = hazard_censoring) # 打ち切りまでの潜在時間
  
  ## --- 全生存期間（OS） ----------------------------------------
  time_os   <- pmin(t_death, t_censoring)
  status_os <- as.integer(t_death <= t_censoring)  # 1 = 死亡, 0 = 打ち切り
  
  ## --- 無再発存期間（RFS） -------------------------------------
  time_rfs <- pmin(t_relapse, t_death, t_censoring)
  
  status_rfs <- integer(n)
  status_rfs[time_rfs == t_relapse & time_rfs < t_censoring] <- 1 # 再発
  status_rfs[time_rfs == t_death & time_rfs < t_censoring] <- 1   # 死亡
  
  ## --- 累積再発率（CIR） + 競合リスク --------------------------
  time_cir <- pmin(t_relapse, t_death, t_censoring)
  
  status_cir <- integer(n)
  status_cir[time_cir == t_relapse & time_cir < t_censoring] <- 1 # イベント1: 再発
  status_cir[time_cir == t_death & time_cir < t_censoring] <- 2   # イベント2: 競合リスクとしての死亡
  
  ## --- データフレームにまとめる --------------------------------
  dat <- data.frame(
    id         = 1:n,
    sex        = factor(sex, levels = c(0, 1), labels = c("WOMAN", "MAN")),
    age        = age,
    stoma      = factor(stoma, levels = c(0, 1),
                        labels = c("WITHOUT STOMA", "WITH STOMA")),
    time_os    = time_os,
    status_os  = status_os,
    time_rfs   = time_rfs,
    status_rfs = status_rfs,
    time_cir   = time_cir,
    status_cir = status_cir
  )
}
library(cifmodeling)
set.seed(46)
dat <- generate_data(hr1=2, hr2=1.5) #再発ハザード比2, 死亡ハザード比1.5のデータ生成
rr_at_5 <- polyreg(nuisance.model=Event(time_os,status_os)~1, exposure="stoma", data=dat, 
                    effect.measure1="RR", time.point=5, outcome.type="survival")
summary(rr_at_5)

                      event 1 (no competing risk)
---------------------------------- 
stoma, WITH STOMA vs WITHOUT STOMA 
                      1.367       
                      [1.006, 1.856]
                      (p=0.045)   

---------------------------------- 

effect.measure        RR at 5     
n.events              89 in N = 200
median.follow.up      3.54        
range.follow.up       [0.03, 28.20]
n.parameters          2           
converged.by          Converged in objective function
nleqslv.message       Function criterion near zero
rr_at_10 <- polyreg(nuisance.model=Event(time_os,status_os)~1, exposure="stoma", data=dat, 
                    effect.measure1="RR", time.point=10, outcome.type="survival")
summary(rr_at_10)

                      event 1 (no competing risk)
---------------------------------- 
stoma, WITH STOMA vs WITHOUT STOMA 
                      1.126       
                      [0.744, 1.704]
                      (p=0.576)   

---------------------------------- 

effect.measure        RR at 10    
n.events              117 in N = 200
median.follow.up      3.54        
range.follow.up       [0.03, 28.20]
n.parameters          2           
converged.by          Converged in objective function
nleqslv.message       Function criterion near zero
rr_at_20 <- polyreg(nuisance.model=Event(time_os,status_os)~1, exposure="stoma", data=dat, 
                    effect.measure1="RR", time.point=20, outcome.type="survival")
summary(rr_at_20)

                      event 1 (no competing risk)
---------------------------------- 
stoma, WITH STOMA vs WITHOUT STOMA 
                      1.078       
                      [0.720, 1.613]
                      (p=0.714)   

---------------------------------- 

effect.measure        RR at 20    
n.events              137 in N = 200
median.follow.up      3.54        
range.follow.up       [0.03, 28.20]
n.parameters          2           
converged.by          Converged in objective function
nleqslv.message       Function criterion near zero

私「ハザード比は一定のデータを作ったのに、リスク比は1.367、1.126、1.078と徐々に小さく推定されてる。冒頭のKaplan-Meier曲線でも、最初の5年あたりがいちばん差が開いているもんね。時間と効果って、分けて考えられないんだね」

お父さん「だってそうでしょ？効果って時間とともに生じるものだもの。それが因果の定義のひとつでもある。時間とともに効果の大きさが変化するなら、ハザード比に頼ることはできない。もっと丁寧に時点ごとにリスクを比べないと」

  • Time-constant effect: 1つのハザード比で全期間を説明する（Cox回帰）
  • Time-varying effect: 効果の大きさが時間とともに変わる（Kaplan-Meier曲線で記述）
  • Time-point effect: ある時点のリスクや生存確率に注目して比べる（polyreg）

私「そういわれると納得感あるなあ、ハザード比だけ使えばいいって方がシンプルで私好みだったんだけど。生存曲線を見るっていうのは、因果効果に時間の視点を加えるってことなんだね」

文献

  • Mok TS, Wu YL, Thongprasert S, Yang CH, Chu DT, Saijo N, Sunpaweravong P, Han B, Margono B, Ichinose Y, Nishiwaki Y, Ohe Y, Yang JJ, Chewaskulyong B, Jiang H, Duffield EL, Watkins CL, Armour AA, Fukuoka M. Gefitinib or carboplatin-paclitaxel in pulmonary adenocarcinoma. N Engl J Med 2009;361(10):947-57

This concludes the Effects and Time series. If you’d like to keep reading over your next cup of coffee, the following episodes are waiting: