Logit: How a Transformation Shapes an Effect

Published

December 8, 2025

Adjusting for Bias III− Logit: How a Transformation Shapes an Effect

Keywords: effect measure, generalized linear model

数式を使ってロジスティック回帰を教えてよ

お父さん「ああ、ここにいたんだ。コーヒーと大福？」

私「うんうまいよ」

お父さん「食べながらでいいから聞いてよ。ロジスティック回帰はね、医学研究でよく使うから知っておいた方がいいと思って。簡単にいうと、2値データのための回帰モデルの一種。ストーマ造設、年齢、性別、年収といった共変量が、復職の有無のような2通りの値をとるアウトカムとどの程度相関するかを、調べることができる」

私「もうちょっと統計っぽく教えてよ」

お父さん「ん？統計手法には、パラメトリック法とノンパラメトリック法があるけど、ロジスティック回帰はパラメトリックモデルの一種として位置づけられる。最近の教科書では、一般化線型モデルのひとつとして扱われることが多いかな」

私「そういうんじゃなくてさ。ほら、リンク関数とか出てきたでしょ。ああいうのがでてくると消化不良でさ」

お父さん「数式使っていいの？」

私「うん。数式でてくると、ところどころわからないんだけど。ごまかされるのもいや。ほら、このペン使っていいよ」

お父さん「じゃあ、個人のリスクと共変量の関係から話せばいいのかな」

ロジスティック回帰

\(N\)人の対象者に番号をつけて\(i=1,...,N\)で表すことにします。個人\(i\)のリスクを\(\pi_i\)で表します。\(\pi_i\)は、個人レベルの\(N\)個のパラメータですが、そのすべてを別々に推定したいわけではありません。\(\pi_i\)に関連する\(p-1\)個の共変量\(X_{i,1},X_{i,2},...,X_{i,p-1}\)が測定されており、両者の関連の強さに関心があるとします。このとき

\(\log(\frac{\pi_i}{1-\pi_i})=\beta_0+\beta_1X_{i,1}+...+\beta_{p-1}X_{i,p-1}\)

という関係が成り立つ確率分布をロジスティック回帰といいます。

この式の係数\(\beta_0,\beta_1,...,\beta_{p-1}\)を回帰係数（regression coefficients）、特に\(\beta_0\)を切片項（intercept）といいます。正規分布は平均と分散というパラメータで形状が決まりますよね。それと同じように、ロジスティック回帰の確率分布は、回帰係数\(\beta_0,\beta_1,...,\beta_{p-1}\)で規定されます。\(\pi_i\)は、\(\beta_0,\beta_1,...,\beta_{p-1}\)が与えられれば計算できますが、直接推定するわけではありません。

私「ふむふむ。ひとりひとりに\(\pi_i\)と\(X_{i,1},X_{i,2},...,X_{i,p-1}\)がある。そしてロジスティック回帰の式で結びついているわけね。そして、その式の係数が回帰係数」

お父さん「そう。ロジスティック回帰の裏には2項分布があって、実は\(\pi_i\)は2項分布の確率に対応している。2項確率の式に、共変量\(X_{i,1},X_{i,2},...,X_{i,p-1}\)が含まれていて、アウトカムと共変量の関連の強さを、回帰係数が決めるんだ」

私「この式まではわかったよ」

お父さん「よかった。ちょっと補足するとね、確率分布に含まれる未知数のことを、統計学ではパラメータと呼んでいる。そしてパラメータの関数として、確率分布を書くことができるものを、パラメトリックモデルっていうんだ。こういう風に考えると、パラメータを推定したり、推定値に信頼区間をつけたりすることが、統計解析の目標になるよね。もうひとつ知っておいてほしいのが、ロジスティック回帰では、アウトカムと共変量の関係がロジット関数（logit function）で結びつくと仮定していること。glm()について話したの覚えてる？」

私「うん。リンク関数をlinkで指定することは理解したよ。それがこの式？」

お父さん「そうだよ。glm()の引数は、family、y ~ x1 + x2、linkなんだけどfamily=binomial()のように 2項分布を選ぶと自動的にロジット関数が使われる。ロジスティック回帰の左辺をみてよ」

リンク関数とロジット関数

個人のパラメータと共変量との関係を結びつける1対1の単調な変換

\(g(\pi_i)=\beta_0+\beta_1X_{i,1}+...+\beta_{p-1}X_{i,p-1}\)

のことを、一般にリンク関数（link function）といいます。ロジスティック回帰のリンク関数は

\(g(\pi_i)=\log(\frac{\pi_i}{1-\pi_i})\)

です。この関数はロジット関数と呼ばれ、ロジスティック回帰を特徴付けています。

ロジット関数の特徴

私「単に関数に名前をつけただけでしょ。もうちょっと解説が欲しいなあ」

お父さん「そうだよね。ロジット関数も関数の一種だから、グラフにした方が特徴がつかみやすい。次の説明だとどうかな」

ロジット関数の形状

仮に共変量が1個で、連続データだったとしましょう。確率\(\pi_i\)と共変量\(X_i\)の関係は、ロジット関数を通じて

\(\log(\frac{\pi_i}{1-\pi_i})=\beta_0+\beta_1X_{i}\)

という式で表されることになります。

図は、このロジット関数の\(\exp(\beta_1)\)の値を5、10、20、200と設定して、\(X_i\)を0から1までの範囲で変化させた、ロジット関数の逆関数のプロットです。\(\exp(\beta_1)\)は、\(X_i\)が1SD変化したときのオッズ比に相当します。つまり、図でもっとも傾きの小さい黒い曲線は、オッズ比5のときのものです。この曲線はそれほど変化が急にはみえませんが、医学研究ではオッズ比5でもかなり強い関連です。

このように、ロジット関数の逆関数はS字型の曲線を表しています。X軸方向にどんな値をとったとしても、Y軸方向の変化は0から1の範囲に収まることが、特徴のひとつです。そして、曲線の傾きは回帰係数\(\beta_1\)によって決まります。

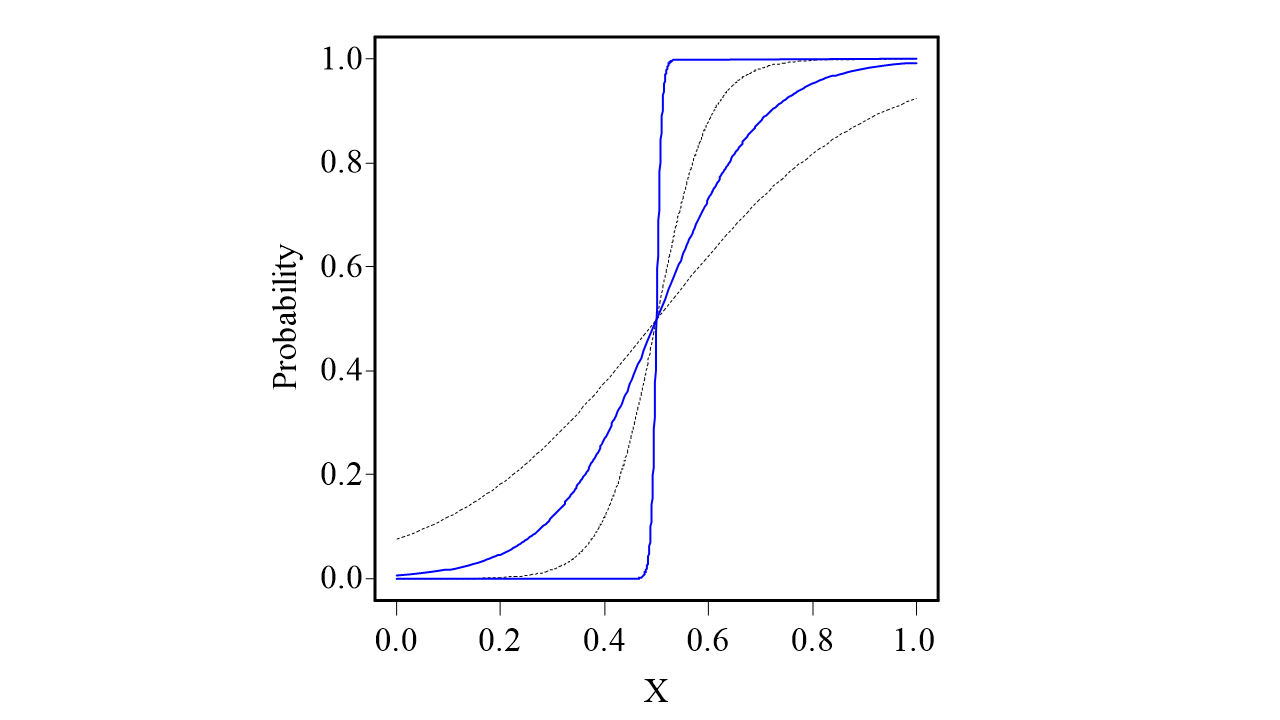
私「やっとイメージがわいた。ロジット関数って、確率と共変量との関係を表してるんだ。どれくらい年齢が上がると、復職できる確率が下がるか、みたいなことね」

お父さん「さらに、ロジスティック回帰は、がんサバイバー調査のように群を比較するときにも使われる。シンプルに2人の対象者を比べるとどうなるかって話をするね」

ロジット関数とオッズ比の関係

共変量が1個のとき、ロジスティック回帰は

\(\log \left(\frac{\pi_i}{1-\pi_i}\right)=\beta_0+\beta_1X_{i}\)

と表すことができます。そして、対象者\(i=1\)では\(X_{1}=0\)、対象者\(i=2\)では\(X_{2}=1\)という値をとる状況を考えてみましょう。それぞれの対象者の共変量の値を、上の式に代入すると、以下のようになります。

\(\log\left(\frac{\pi_1}{1-\pi_1}\right)=\beta_0\)

\(\log\left(\frac{\pi_2}{1-\pi_2}\right)=\beta_0+\beta_1\)

ここで、\(\pi_1\)は対象者1の確率パラメータ、\(\pi_2\)は対象者2の確率パラメータです。これらの確率パラメータから、オッズ比を求めるとどうなるでしょうか。それは、以下の式で計算されます。

\(\left(\frac{\pi_2}{1-\pi_2}\right)\div\left(\frac{\pi_1}{1-\pi_1}\right)=\exp(\beta_0+\beta_1)\div \exp(\beta_0)=\exp(\beta_1)\)

この結果は、回帰係数\(\beta_1\)の指数をとるとオッズ比が得られることを意味しています。

私「なるほど、回帰係数からオッズ比を計算できるってこういうことなのね」

お父さん「このオッズ比の計算ができるのは、ロジット関数の特徴によるものでしょ。だから、ロジスティック回帰はオッズ比のモデルともいえるんだ。リスク比にはリスク比のモデルがあるし、リスク差にはリスク差のモデルがある。大事なのはfamily、y ~ x1 + x2、linkを選ぶことで、データの型にあった回帰モデルを指定できるってこと。yとxにそれぞれ連続変数を指定すると、散布図に回帰直線を掛くことができるし、計数データにPoisson回帰を当てはめたりもできる。一般化線型モデルは、生存時間データや経時データ以外ならほとんど対応できる汎用的な統計手法なんだ」

ロジスティック回帰の可逆性

私「でもね、その説明だとみんなロジスティック回帰を使ってる理由にはなってないよね。link="logit"よりlink="identity"、つまり変換しなくたっていいじゃない」

お父さん「それはリスク差のモデルだね。そのモデルが悪いわけじゃないけど、ロジット関数が選ばれた理由はちゃんとある。この話はちょっと抽象的かもしれない。たとえるならね、ロジスティック回帰はルービックキューブのように構造が安定しているんだ」

私「どういう意味？」

お父さん「操作を加えても構造が維持されるっていうこと。どんな方向で、どんな順序で面を回しても、ルービックキューブは元に戻せる。解けば絵の向きもきちんと揃う。観測できるのは、ただの1面しかないんだけどね」

私「ロジスティック回帰とルービックキューブねえ」

お父さん「統計解析に話を戻そうか。人工的にデータに変換を加えることがあるよね。たとえば死亡じゃなくて生存をアウトカムにしたり、LDLコレステロールの単位をmg/dLからmmol/Lに変えたり。これは共変量\(X_i\)のスケール変換のことだよ」

私「うんうん。それはよくやることだよね」

お父さん「統計学者は、いろいろな回帰モデルのうち、変換に対して不変な構造はなにかって考えた。ここでいう変換は、数学では群作用（group action）っていうんだけど、ある変換を加えても意味が変わらない操作のこと」

私「出た。抽象。なんだそれ」

お父さん「ほら、コインの表裏を入れ替えてもコイン投げの確率は変わらない。ルービックキューブを回転しても構造は変わらない。考えた結果、2値アウトカムのモデルでは以下のパーツを使うしかないってことがわかった」

  • 確率分布: 2項分布（指数型分布族）

  • 回帰係数×共変量（線型結合）

  • リンク関数: ロジット関数

お父さん「ここで出てくるロジット関数は、変換しても可逆性（invertibility）を保つ唯一の関数なんだ。たとえば死亡確率を\(\pi=0.2\)とするよ。このとき生存確率は？\(1-\pi=0.8\)だよね」

私「うん。当たり前」

お父さん「この”死亡と生存を入れ替える”という操作が群作用に相当する。ここで問題にしているのはリンク関数\(g\)だったよね。確率\(\pi\)を、リンク関数で別のスケール\(g(\pi)\)に変換したとする。このとき、死亡と生存を入れ替えても、値が反転するだけで構造が維持されるには\(g\)はどんな性質を持つべき？」

私「なるほどね、そういう意味で可逆性っていってるのね。でも値が反転するってのがわかんないな。どういうこと？」

お父さん「つまりこういうこと」

\[g(1−\pi)=−g(\pi)\]

私「へ？やっぱ意味わかんない」

お父さん「さっき、対象者1の\(\pi_1\)と対象者2の\(\pi_2\)を比べるとオッズ比が出てきたのを思い出して。あのとき、\(g(\pi_1)\)と\(g(\pi_2)\)の差をとっていた。\(g\)じゃなくてロジット関数そのものを使ったけどね。つまり、\(g(\pi)\)は差のスケールで死亡リスクがどれくらい高いかを表す尺度なんだ。死亡と生存を入れ替えたらどうなる？\(g(1-\pi)\)は死亡リスクの低さを意味するよね。つまり、死亡と生存の入れ替えによって、符号は反転するはず」

私「なるほど。\(g(1−\pi)=−g(\pi)\)という関係が成り立つのはなにか探せばいいのね？」

お父さん「もう少し条件がある。さっきいった共変量の変換でも関係性は維持されるっていう条件がそのひとつ。また、\(g(\pi)\)という尺度に、上限と下限があったら不便だし、ゼロという基準が必要だよね。だからさらに条件を追加する」

  • \(g(1−\pi)=−g(\pi)\)
  • \(\pi\)が0に近づけば\(g(\pi)\)は−∞に向かう
  • \(\pi\)が1に近づけば\(g(\pi)\)は∞に向かう
  • \(\pi=1/2\)を基準にとって\(g(1/2)=0\)

お父さん「この4つの条件を満たす滑らかな関数は、実はほとんどひとつしかない」

\[g(\pi)=\log \left(\frac{\pi}{1-\pi}\right)\]

私「それがロジット関数ってことか。データを人工的に変換しても解析結果が変わらないってこと？」

お父さん「あれ、そこまでは説明しなかったけど、その通り。可逆性があるモデルでは、データを変換しても構造もそれに合わせて変わってくれて、本質的に同じ解析結果が得られる。みんなが使っている統計手法はね、大半が人間が選んだだけじゃないんだ。数学的な法則がそっと姿を現しているんだよ」

このエピソードに関係するクイズです

脳卒中発症の有無をアウトカム、LDLコレステロールを共変量としてロジスティック回帰を当てはめたとします。LDLコレステロールの単位をmg/dLからmmol/Lに変換したとき、オッズ比は何倍になるでしょうか。ただし

LDLコレステロール(mmol/L) =LDL コレステロール(mg/dL) ×0.02586

という関係が成り立ちます。

  1. 0.02586倍
  2. 1/0.02586倍
  3. 変化しない
  4. 1、2、3すべて誤り

正解は4です。

これは単位を換算するにはどうすればよいかという問題です。ある共変量Xの効果は、回帰係数βとの積（βX）で表され、それは共変量の単位によらず一定ですよね。このことに気づくと、答えに近づきます。Xの単位を定数倍すると、βは定数分の一に換算されます。ただし、ロジスティック回帰では、回帰係数からロジット関数を経由してオッズ比を求めるため、単位を換算するには、1/0.02586乗のようにべき乗の操作をすることになります。

文献

次のエピソードとRスクリプト