私「連続データって、年齢とか血圧みたいな測るやつでしょ?2値データもわかるよ。私の調査で比較したいストーマ保有あり・なしとか」
お父さん「ご名答。で、計数データは、交通事故の発生件数のような、数をカウントしたデータのこと。生存時間データは、たとえば寿命とかだね。死亡など特定のイベントが起こるまでの時間を扱うデータだよ。今回のがんサバイバー調査でいえば、手術から復職までの時間とか、再発までの時間とかね」
私「いわれてみれば、たしかに種類が違うね。でも、昔受けたRの授業では、言われた通りにコード打ってただけだったなあ。glm()とかsurvfit()とか、なんかよくわからないことばを」
お父さん「パソコン。あるでしょ。RStudioインストールしよう」
私「はあ、まあ声を掛けたのはこっちだからいいけど」
お父さん「Rではね、連続データを解析するなら、mean()、t.test() なんかがよく使われる」
お父さん「2値データを集計するときはtable()。p値を計算するときはfisher.test()。複雑な解析はglm(family = binomial) みたいな回帰モデル。生存時間データだと、survfit()、coxph()、それからcifplot()みたいな関数が出てくる」
そんなにいっぱい覚えられるわけないでしょ。Rの授業でも思ってたけど、そんなのあたかも呪詛なんだって」
お父さん「大事なのは、どの型のデータに、どんなR関数をあてるのかをイメージできること。もっといえば、どんな確率分布を仮定しているかを、なんとなくでいいから思い浮かべてほしいんだ」
お父さん「学部でやったでしょ。正規分布(normal distribution)は聞いたことある?2値データの2項分布(binomial distribution)は?」
お父さん「単なるデータの記述より高度な統計手法では、裏でなんらかの確率モデル(probability model)を考えてる。生存時間データだと、標準的に使われるモデルってわけじゃないんだけど、一番シンプルな分布は指数分布(exponential distribution)っていうんだ」
お父さん「そうだね、人間が使う言葉とは思えないとはこっちも思うよ。でも、本題に入る前につまづいたらもったいない。もし、統計でわからない言葉が出てきたら、“参考資料”をみてよ。まあ、とにかく、どのデータの型にどんな確率モデルを使うのか、パターンを知ることだね」
お父さん「うん。たとえばさ、これは覚えてほしいんだけど、割合(proportion)と率(rate)っていう指標がある。日常生活でもよく使うでしょ?交通事故の発生率とか。でも、日常では、割合と率の違いを意識しないよね。でも、統計の世界では、割合は2項分布のパラメータ、率はPoisson分布っていう別の確率分布のパラメータなんだ。Poisson分布は少しマニアックだけど」
お父さん「違う違う。割合ってパーセントで表すでしょ、女性割合が60%とか。でも、“東京都の1年あたりの交通事故の発生率”を例に考えてみてよ。パーセントにならなくない?交通事故が何回、起きたかを年で割ってるだけだから」
お父さん「教科書どおりじゃなくていいんだ。“あ、これは正規分布っぽい連続データだから、このあたりの関数かな”とか、0/1のデータだから、このへんの関数かなって、感覚で結びつけられるといいよ。そうするとRの関数もずっと覚えやすくなる」
私「なるほどね。データの型と分布をイメージできれば、R関数丸暗記不要ってことね。そいつははかどるわ」
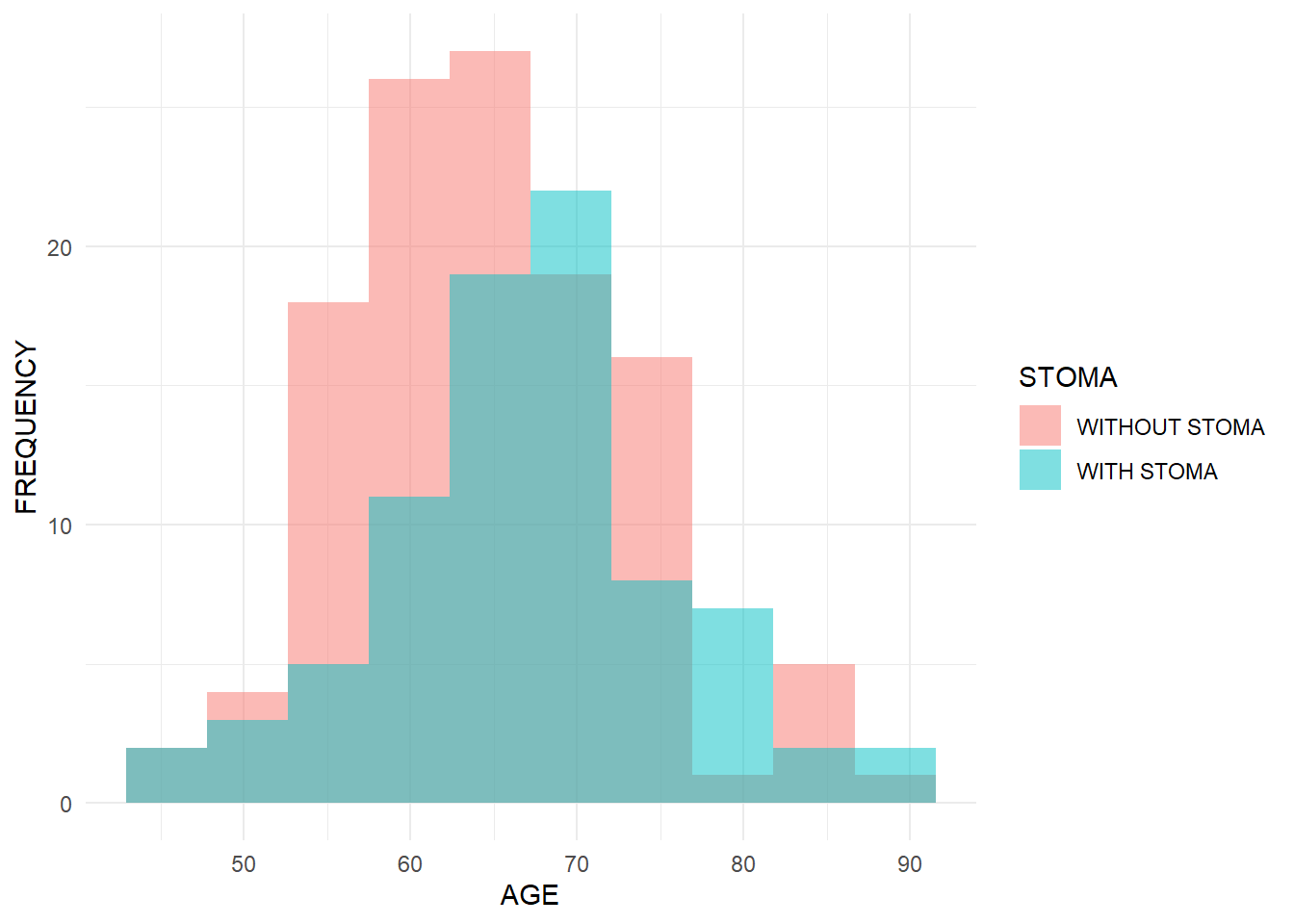
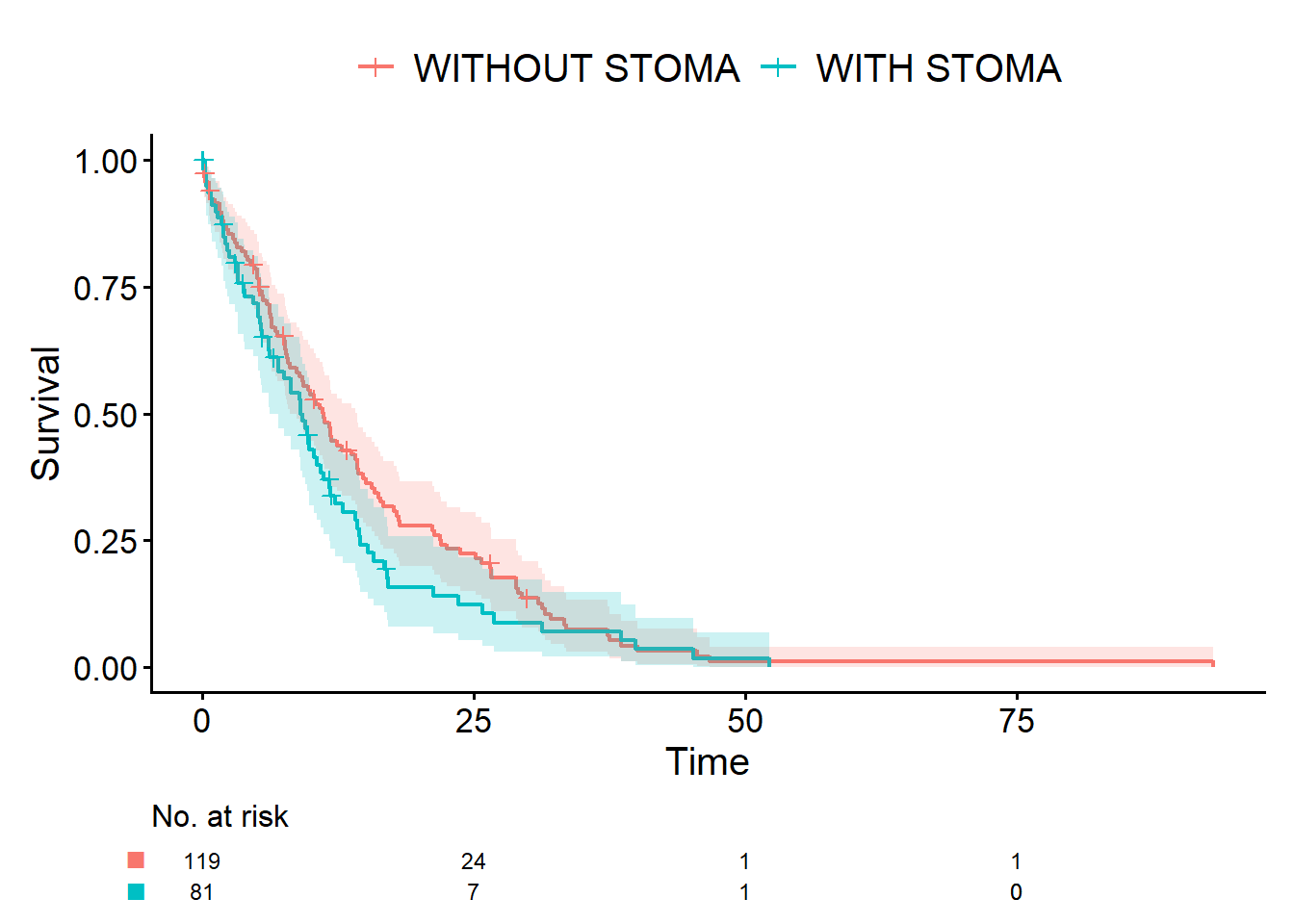
お父さん「そうそう。イメージがあれば、あとでマニュアルや本を見たときに、ああ、これのことかってつながるからね。じゃあ、Rでちょっとだけデモを見せてみようか。年齢(連続)、性別とストーマ(2値)、生存時間(生存時間データ)をシミュレーションして、簡単な解析をやってみるよ。使うのは正規分布、2項分布、指数分布」
お父さん「そうだね。とりあえずlibrary(ggplot2)、library(cifmodeling)って打って。ヒストグラムとKaplan-Meier曲線を教えるよ」
お父さん「教えてあげてるんだから思考停止しない。Rの機能を追加するとき、install.packages()とlibrary()を使う。ざっくりいうとね、それぞれ、“Rパッケージをパソコンにインストールする”コマンドと、“インストール済みのパッケージを使えるようにする”コマンドなんだ」
私「ふむふむ。じゃあインストールの方は、一度やったら、それで終わり?」
お父さん「基本的にはそう。同じパソコンなら、インストールは原則1回でOK。たとえば、install.packages("ggplot2")は、CRANっていうパッケージの倉庫から、自分のパソコンにダウンロードする。library(ggplot2)は、ggplot2を取り出して、“これからグラフを描くからこの道具を使います”ってRに宣言する」
私「なるほど。ちょっとスッキリした。今まで毎回インストールしなきゃいけないのかなって思ってた」
お父さん「毎回インストールすると、“コーヒー淹れるたびに豆を買いに行く”ようなものだからね。豆はまとめて買っておいて、飲むときに挽けばいい。パッケージも同じだよ」