Three-Variable DAGs: The Smallest Building Blocks of Causal Structure

Causal Inference I − Three-Variable DAGs: The Smallest Building Blocks of Causal Structure

Keywords: causal model, clinical trial, confounding & collapsibility, observational study

はじめて研究に取り組む娘と統計家の父。父に研究仮説は”PICO”を”PECO”で整理するといいとアドバイスされ、医師である娘は、がんサバイバーにおけるストーマ造設と復職状況の関係を調査することに決める。父に教わるが、娘はいまひとつ腑に落ちないのだった。

第3の因子なんて無数にあるよね？

お父さん「おはよう。だいぶ寒さが和らいできたね」

私「あ、やっと起きたの。聞きたいことがあったんだ。この前、コーヒーと膵がんの話をしてくれて、ロジスティック回帰で”調整する”っていう操作がどういうことかはわかったよ。確率モデルと因果モデルの違いも納得した。でもさ、問題は”喫煙”を調整するのが正しいかどうかなんじゃない？値が変わったってだけじゃ、説明としては足りない気がするし、Rubin因果モデルの話をしてくれたときもそこには触れなかった」

お父さん「そうだね。前にいったようにデータだけからは、調整前と調整後のどちらが”正しい”かは決められない。でも膵がんの例だと、喫煙は発がん因子だっていう医学的な常識があるよね。こういう事前知識が、調整すべきか交絡因子を選ぶときの判断材料になる。リスク因子だとわかっているなら、疾患にかかる確率をモデル化するときに考慮しておきたいってのは自然だよね」

私「なるほど。その説明なら、まずまず納得できるかも」

グラフで考える

お父さん「本当はね、Rubin因果モデルではなくって図で描いて整理するんだ。ちょっとペンをとってくれる？今、こんなふうに変数が3つあるでしょ。その場合の変数間の因果関係を矢印で表すとき、3パターンあると思わない？この図のように。Eは曝露変数（exposure）、Dはアウトカム（disease）を表していて、E→Dは両者が原因と結果の関係にあるって意味だよ。Cは第3の因子のこと」

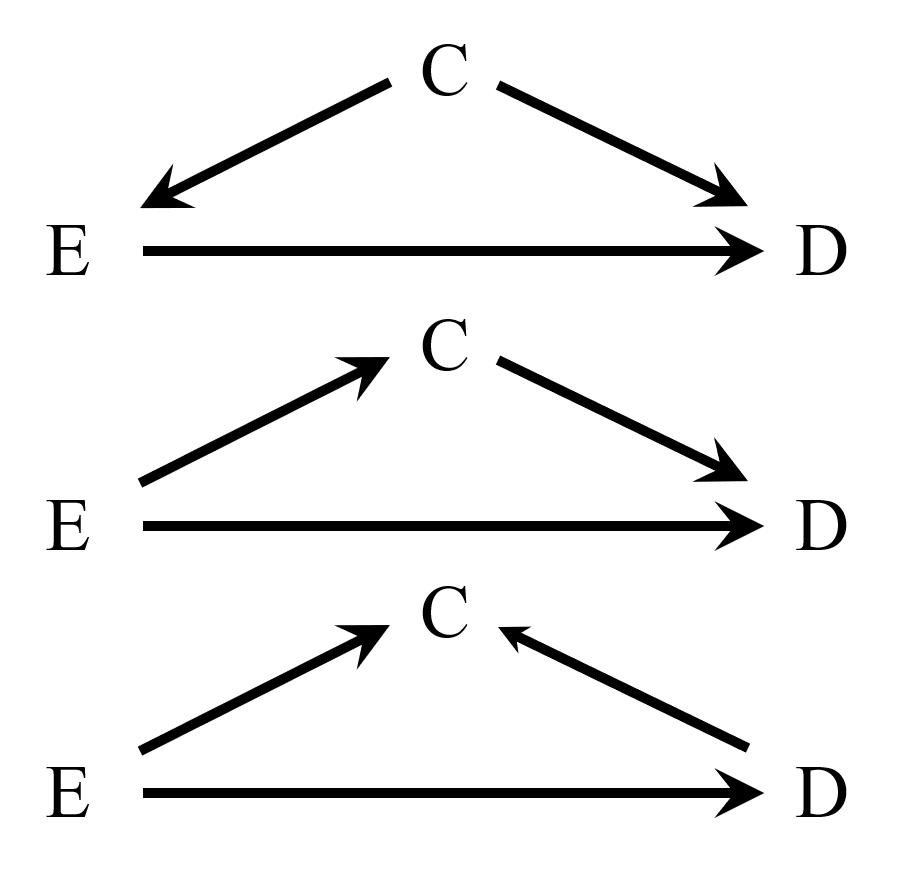
私「この3つは、Cの周りの矢印の向きが違うわけね。確かに、E←C→DとE→C→DとE→C←Dの3パターンで一通りカバーできてるのかな。E←C←Dみたいに、結果から原因に矢印がさかのぼるのは変だし」

お父さん「その通り。その場合、Eが原因、Dが結果だとすると、矢印がぐるっと循環する図は、ふつうは除外する。こういう図は、非循環有向グラフ（DAG）と呼ばれていて、図のCには、それぞれ別の名前と役割を持っているんだ」

  • 共通原因 （common cause）: E←C→DにおけるCのように、曝露変数とアウトカムの両方に向けた矢印を持つ因子
  • 中間媒介因子 （intermediator）: E→C→DにおけるCのように、曝露変数からアウトカムに入る矢印の途中にある因子
  • 合流点 （collider）: E→C←DにおけるCのように、曝露変数とアウトカムからの矢印が合流する因子

お父さん「なにか”がんのリスク因子”をひとつ思い浮かべてみて。それは3パターンのうちどれに当てはまりそう？」

私「えっと、ピロリ菌とか、お酒とか？どっちも発がんリスクを上げるんだから、共通原因か、中間媒介因子のどっちかかな。リスク因子ってことは、D（がん）の向きの矢印を持っているよね」

お父さん「その通り。さらに中間媒介因子について考えてみてよ。中間媒介因子って、曝露がアウトカムに影響する効果の一部を担っているよね。たとえば喫煙によってニコチンに曝露されるけど、ニコチンは”たばこを吸った結果”生じる因子であると同時に、がんの直接のリスク因子でもある。だから、“喫煙の総合的な効果”を推定したいときに、ロジスティック回帰でニコチンを調整するのはおかしいってことになる。ニコチンは効果の一部そのものだから。この理屈でいくと、3パターンのうち、調整すべきなのは共通原因だけという理屈になる」

私「へー。まあパターン分けできそうなのはわかるけど、第3の因子なんて無数にあるよね。思考停止で、全部調整したらいいじゃんって気もするけど」

お父さん「実際にデータを解析するときにはそうはいかない。データに限りがあるし、推定も不安定になるからね。じゃあ次に、ストーマ造設と復職率の調査を考えてみようよ。Eはストーマ造設、Dは復職だよね。たとえば、結腸がんと直腸がんで復職率は違うと思う？」

私「わかんないな。あんまり違わないのかもしれない」

お父さん「仮にがん種の違いは、復職率に直接効いてこないとするでしょ。そして、結腸がんだとあまりストーマを増設しないとしたらどうだろう。C→Eの関係はあるけど、C→Dの関係はないってことになる。このDAGによるとがん種は共通原因じゃないから、調整しなくてもいいってことになる」

私「なるほど、その仮定が正しいならそうね」

お父さん「以前みせてもらった集計では、ストーマ保有者は、非保有者に比べて、平均年齢が低くて、女性が多かった」

私「そうだよ」

お父さん「きっと、60歳を超えると定年の方が多くなるだろうし、男性の方が復職を希望しているんじゃない？こう考えると、年齢・性別は、ストーマ造設と復職率の両方に関連していて、共通原因と考えてよさそうだよね。だから年齢・性別はロジスティック回帰で調整すべきなんだけど、あのときはデータが足りず、モデルが不安だった。つまり、実際の解析では、調整する変数を絞っていかないとうまくいかない」

私「ああ、あのときはそういう思考回路だったのね。お父さんがなにを考えていたか理解できた気がする」

ランダム化の下で第3の因子はどうする？

お父さん「この考え方はランダム化臨床試験でも応用できる。JCOG9502っていう臨床試験の論文を読んだことがあったよね（Sasako, et al. 2006）。あれは、手術方法（TH群またはLTA群）を比較して全生存期間に差があるかを調べた研究だった」

私「うん。だけど、ランダム化しているから第3の因子ってないんじゃない？だってTH群とLTA群をランダムに割付けてるもの」

お父さん「正解。でも、この試験ではハザード比を求めるとき、いくつかの変数を調整している。使ったのはロジスティック回帰じゃなくてCox回帰だけどね。」

私「そうなのか。じゃあ調整した方がいいのかな、さっきの”共通原因だけ調整”の話と矛盾するけど」

お父さん「ここでもDAGを使って考えられる。Eを手術方法、Dを全生存期間、Cをステージとすると、図はこうなる。試験結果では有意な関連はなかったけど、わかりやすいようにE→Dの矢印は残したよ」

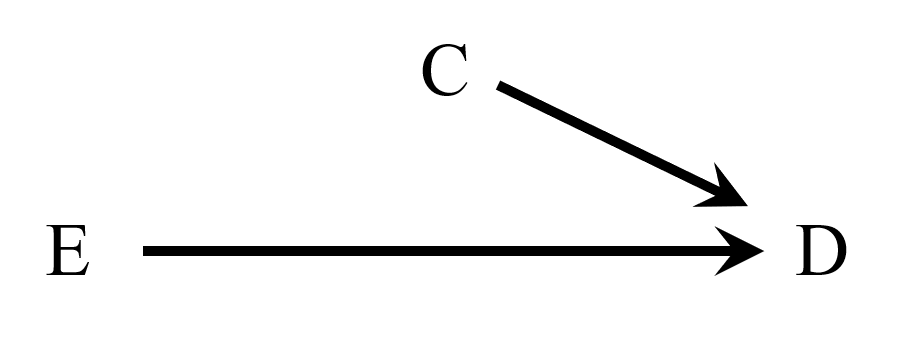
私「やっぱり共通原因ではないね」

お父さん「そう。ステージは交絡因子ではないから、調整する必要はなかった。でも、Cox回帰によって全生存期間をモデル化するとしたらどうかな。がんのステージはもちろん予後に関係するから、モデルに入れたくならない？」

私「それは入れたくなる。ステージだけじゃなくてリンパ節転移とか、残存腫瘍の有無とかもモデル化したくなる」

お父さん「この図の場合、Cは交絡因子じゃないから、調整しなくてもバイアスは生じない。でも、真に近いモデルを当てはめて、ハザード比の推定精度を高めるという観点からは、Cを調整してもいい」

  • 交絡因子を調整する目的: 因果効果推定におけるバイアス補正

  • 回帰モデルに共変量を加える目的: 確率モデルのデータへの当てはまりの改善（結果的にバイアス軽減につながる）

お父さん「じゃあ、JCOG9502の論文を読んで、調整した変数をリストアップしてよ」

私「ほい」

  • ステージ
  • Borrman型
  • 残存腫瘍
  • リンパ節転移（傍大動脈）
  • リンパ節転移（縦隔）
  • リンパ節転移（陽性数）
  • 洗浄細胞診

お父さん「このうち術前に確定するものと術中・術後変数はどれなの？術中・術後変数の変数はさっきのDAGとは違い手術の影響を受けるから、E→Cの矢印が必要だよね」

私「そうだね、残存腫瘍、リンパ節転移、洗浄細胞診あたりは手術の途中から後に決まるかな。特に残存腫瘍なんかは」

お父さん「じゃあ残存腫瘍を考えよう。Eを手術方法、Dを全生存期間、Cを残存腫瘍とするとDAGはこうなる」

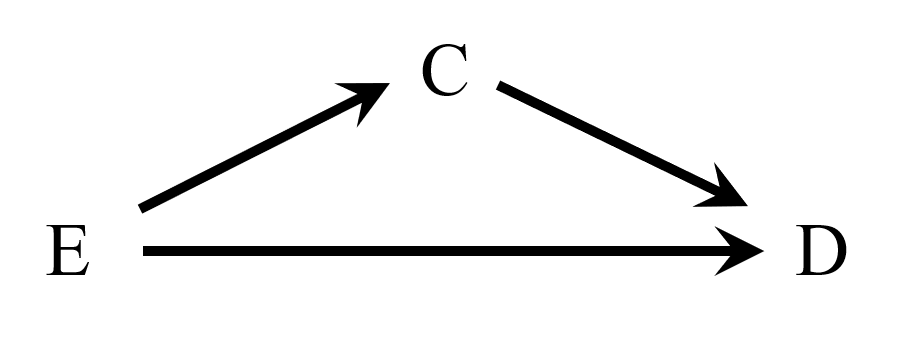
私「中間媒介因子だね」

お父さん「うん。DAGを用いて交絡因子を選ぶとしたら、残存腫瘍は交絡因子でないから、Cox回帰で調整しないことになる。この研究では、アウトカムを正しくモデル化するという観点から調整変数を選んだみたい。でも中間媒介因子は調整しない方が、純粋に術式の違いだけがもたらす因果効果が得られるから結果の解釈はしやすい」

このエピソードに関係するクイズです

この2つのDAGの解釈として正しいのはどれでしょうか。

  1. どちらの図にもEとDに因果関係がある
  2. 上図はEとDに因果関係があるが、下図にはない
  3. 下図はEとDに因果関係があるが、上図にはない
  4. どちらの図にもEとDに因果関係はない

  • 正解は1です

どちらも中間媒介因子ですが、上の図では、E→Dという直接の因果関係がありますよね。下の図でも、EはCに作用し、CはDに作用する関係があります。つまり因果関係はないというのは言い過ぎで、間接的な因果関係があるという解釈が正解になります。

文献

  • Sasako M, Sano T, Yamamoto S, Sairenji M, Arai K, Kinoshita T, Nashimoto A, Hiratsuka M, Japan Clinical Oncology Group (JCOG9502). Left thoracoabdominal approach versus abdominal-transhiatal approach for gastric cancer of the cardia or subcardia: a randomised controlled trial. Lancet Oncol 2006;7(8):644-51

次のエピソード