A Subtle Distinction between Common Causes and Confounders

Published

December 13, 2025

Causal Inference II − A Subtle Distinction between Common Causes and Confounders

Keywords: bias, causal model, confounding & collapsibility, observational study

DAGと一般因果

私「お父さん、共通原因がバイアスってのはわかるんだけど、正直コーヒーと膵がんの話からあんまり進歩した気がしないんだ。その理由はふたつある。まず、私たちが調べてるのは個々の出来事じゃなくて一般法則だよね」

お父さん「うん」

私「でも、JCOG9502でステージと術式が独立だったのは、ランダム化したからでしょ。それって人工的じゃない？実地医療ではステージと術式は関連するもの。これでいいのかな。今回のDAGっていう矢印を使った図、普遍的じゃない気がする。コーヒーと膵がんのときは違和感なかったんだけど」

お父さん「それはランダム化臨床試験が実験的環境を反映しているからかもね。実際、DAGが示している関係は、あくまで研究から得られたデータを反映するもので、どんな環境でも成り立つとは限らない」

私「それにさ、いままでのDAGは3変数しかないけど単純すぎない？現実はもっと複雑だよね」

お父さん「もちろんDAGの変数を増やすこともできるよ。そうすると、もっと統計学っぽい理屈になっちゃうけど」

私「そうなんだ。でもごまかさず説明くらいしてよ」

お父さん「じゃあ変数を5つに増やした例を使って、もう少し正式に解説してみようか。それにはちょっとコーヒーがほしいな」

後ろ扉を閉ざすなんて映画みたい

NoteDAGの例

因果関係の例として、ピロリ菌と胃がんを取り上げます。このふたつの変数には、抗生物質を飲んでピロリ菌を除菌することで、胃がん発生を予防できることが知られていますよね。言い換えると、ピロリ菌除菌は「原因」、胃がん発生は「結果」に対応します。

しかし、胃がんに関連する変数は、これだけではありません。たとえば、若いうちは胃がんにはなりませんが、高齢になると胃がんリスクが高くなりますし、同じ年齢でも胃の炎症など様々な体質の違いが胃がんの発生に関連することがわかっています。これを踏まえて、以下の3つの仮定を置くことにします。この仮定は必ずしも正しいわけではなく、あくまで説明のための題材です。

  • 年齢が高くなるにつれ、胃がんリスクは高くなるが、その一部は胃の炎症の程度に反映される。胃の炎症がひどくなると、胃がんにかかりやすくなり、さらに医療機関に受診して、ピロリ菌を除菌してもらう確率が高くなる
  • 心配性な人もまたピロリ菌除菌を受けやすい。心配性な性格だと、胃の炎症も起こしやすい。ただし、性格はピロリ菌除菌と胃の炎症への影響を通してのみ、胃がんに関連する
  • 年齢、性格、体質、ピロリ菌以外に、胃がん発生に関連する重要な変数はない

5つの変数をAからEまでの記号で表すと、上の3つの仮定は、以下のようなDAGで表現できます。

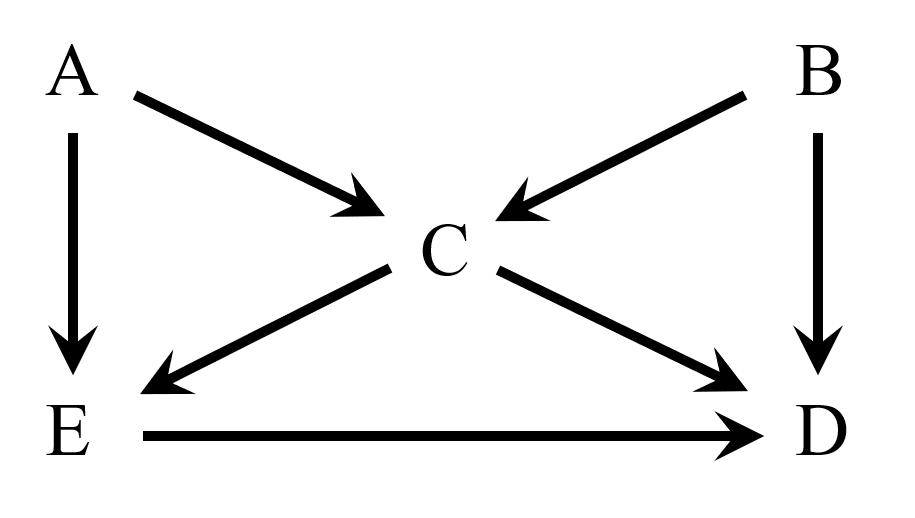
  • A: 性格（心配性）
  • B: 年齢
  • C: 体質（胃の炎症）
  • D: 胃がん発生
  • E: ピロリ菌除菌

お父さん「前回の話を思い出しながら、このDAGを考えてみてよ。交絡因子として調整しないといけない変数はどれだろう」

私「ん？共通原因、中間媒介因子、合流点っていう3パターンがあったんだっけ。共通原因を見つければいいから、Cかな。いや、真に近いモデルを当てはめる、なんてことも言ってたよね。だからBとC。どうかな、あってる？」

お父さん「結果論だけどあってる。実はね、このDAGはトリッキーで、Cを調整するだけじゃ、バイアスが残る例なんだ。まず、DAGのそもそもの意味は、directedつまり有向パスだけで構成された、acyclicな循環していないグラフっていうこと。つまりDAGでは、ノード間の結びつきがすべて矢印で表されて、しかも矢印がループ状にぐるぐるまわったりしない。そして、有向パスと共有原因を経由するバックドアパスの2種類に注目してほしい」

私「ふむ」

お父さん「有向パスっていうのは、A→B→C→Dのような矢印で連鎖しているノードの集合のこと。これはAからDの順に因果関係が伝わることを意味している」

私「ふむふむ。バックドアパスってなに？」

お父さん「あるノードに注目してみて。このノードに入る矢印を通じたパスのこと。矢印は出るか入るかしかないでしょ。バックドアパスは、原因に矢印が入る方向から回り込むような経路なんだ」

私「ああ、バックドアっていうから後ろ扉かと思った。後ろ扉を閉じて地震を防ぐっていう映画があってね」

お父さん「ふーん。とりあえず、有効パスでは矢印が出る、バックドアパスでは矢印が入る、ここをみてみよう」

私「えっと、とりあえず胃がんのやつをみるね。このDAGには、EとDを結ぶパスは、両者を直接結び付ける有向パスが1つ、バックドアパスが4つある（E←A→C←B→D、E←A→C→D、E←C←B→D、E←C→D）」

お父さん「そうでしょ。そして、バックドアパスは、必ず共通原因Cを経由している。これがDAGの特徴のひとつ。前回の説明を思い出してみて。共通原因は交絡因子として調整すべきっていったよね。DAGが複雑になると、バックドアパスが増えるけど、基本は同じ。すべてのバックドアパスをブロックできるような共通原因を探して、調整すればいいんだ。共通原因はDAG上のどこにあるかの話、交絡因子はブロックすべき変数の話ってこと」

Noteバックドア基準

あるDAGが与えられたとき、どのノードを交絡因子として調整すればじゅうぶんなのかを判断するための基準のひとつがバックドア基準です。原因と考えているノードをE、結果と考えているノードをDとします。DAG上のノードの集合Sが以下の条件を満たすなら、Sを交絡因子として調整すればじゅうぶんです

  • EからDへの合流点を含まないバックドアパスは、Sによりブロックできる
  • EからDへのバックドアパス内に合流点あり、それがSに含まれるか、Sの子孫だとする。このときSは、そのバックドアパス内の非合流点を含まなければならない

お父さん「厳密にいうと、バックドア基準っていう上のようなルールを使うんだけどね。合流点・ブロックについては、後で説明するよ。要は、共通原因を調整して、バックドアパスをブロックすれば、バイアスを防ぐことができる。疫学ではDAGは交絡因子を探すために用いられるんだ」

私「やはり要石で後ろ扉を閉じるみたいな話だったか」

NoteDAGの用語

次に、DAGで用いられる用語を整理しておきます（Greenland, Pearl, Robins 1999）。ここで説明する用語は、ノード、矢印、有向パス、バックドアパス（backdoor path）、祖先と子孫です。

グラフ上の変数を表す点を、ノードといいます。上のグラフには5つのノードがありますよね。2つのノードは、線や矢印で結ばれます。A→Bという矢印で結ぶと、それはAからBへの方向性があることを意味します。因果推論の文脈では、原因から結果への直接的な結びつきを表しています。このグラフでは、AとCは隣接しているが、AはBやDとは結ばれていません。これは、AのCへの直接的影響があるという意味です。直接的影響があるとは、もっというと、グラフ上の他の変数に媒介されない影響がある、ということです。

胃がんの例では、性格は、ピロリ菌除菌と体質を通じて胃がん発生をもたらすと仮定しました。この仮定は、AからBやDへの矢印がないことに対応しています。

矢印で結びついたグラフは、必ず、矢印の頭から入り、頭から出るような一続きの矢印で辿ることができます。直接的または間接的にノードを結びつける矢印の組み合わせのことを、パスといいます。特に、矢印の方向に従って辿ることのできるパスを、方向性のあるパスという意味で有向パスと呼んでいます。上のグラフでは、A→C→Dのパスは有向パスです。

次にE←C→Dについて考えてみましょう。こちらは有向パスではありません。有向パス以外のものを無向パスといいます。

無向パスのうち重要なのは、あるノードから矢印をさかのぼって出て、別のノードに入るパスです。これをバックドアパスといいます。このグラフでは、EからDへのパスは、直接のパス以外はすべてバックドアパスです。

そして、あるノードを出て別のノードに入っていく有向パスがあるとき、前者を祖先、後者を子孫といいます。文献によっては、祖先を原因、子孫を結果と呼んでいることもあります。このグラフでいえば、A、B、Cは、すべてEとDの祖先です。逆に、EとDは、A、B、Cの子孫です。そしてEはDの祖先であり、DはEの子孫です。

Noteこのエピソードに関係するクイズです

下のDAGにおいて、破線で示したパスA-C-Bに注目してください。このパスにおいて、Cは次のうちどれでしょうか。

  1. 中間媒介因子
  2. 共通原因
  3. 合流点
  4. 1、2、3のどれでもない

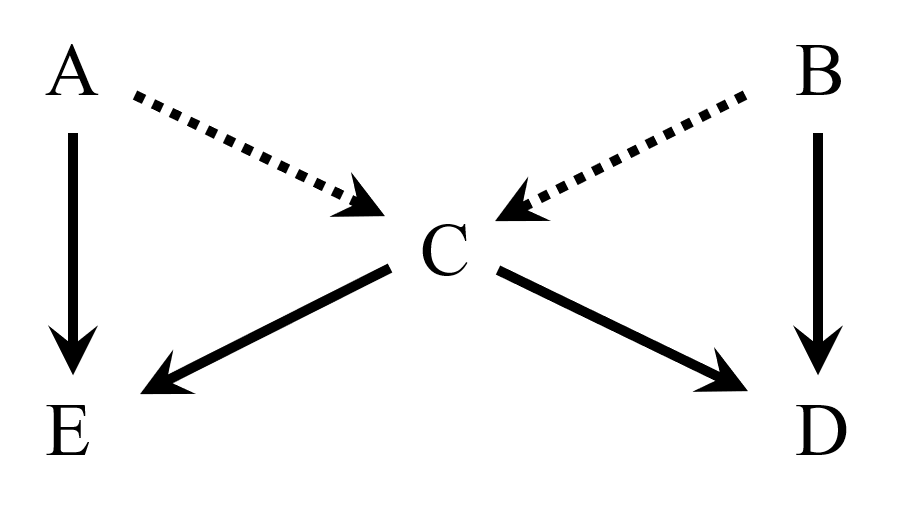
  • 正解は3です。

ここで注目してほしいのは、Cは共通原因でもあり、合流点でもある、という点です。このようなとき、機械的にCだけを調整すればいいと、判断することはできません。バックドア基準を使うべきです。

詳しくは次回述べますが、もし理由を説明するなら、以下のようになります。パスE←A→C←B→Dに注目してください。このパスは合流点Cを含むため、なにも調整しなくてもブロックされています。つまり、これだけをみると、Cは調整しなくてもよいのです。

その一方で、パスE←A→C→Dについて考えると、AもCも合流点ではありません。つまりこのパスは、なにも調整しないとブロックされていないのです。つまり、このDAG全体でみると、EとDには相関が生じています。さらに、E→Dという因果関係はないことから、この相関は疑似相関です。したがって、なにも調整しなくていい、という判断も間違いです。

文献

  • Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology 1999;10(1):37-48

次のエピソード