Backdoor Paths, Block, and d-Separation: A Clue for Adjusting for Bias

Causal Inference V − Backdoor Paths, Block, and d-Separation: A Clue for Adjusting for Bias
Keywords: bias, causal model, confounding & collapsibility, probability model
ブロックの意味
私「この前の続きをやろうよ、お父さん。DAGを説明してくれたときにさ、ブロックって用語が出てきたでしょ。合流点がパスをブロックするとか」
お父さん「出てきたね」
私「あれって、因果の流れが止まるって意味だよね」
お父さん「うーん、その言い回しは厳密じゃない気がするなあ。ブロックは、DAG上のパスの性質について述べたもので、因果関係とは直接関係ない。パスが合流点を含んでいたり、非合流点を交絡因子として調整したりすることを指すんだけど」
私「合流点があると、そのパスはなにもしなくてもブロックされる。非合流点については、調整するとパスがブロックされるってことね」
お父さん「うん。専門的には、パスをブロックすると、ノードとノードを”有向分離”できるっていうのがポイントなんだけどなあ。有向分離の定義にも触れておいた方が誤解がなさそうだね」
DAG上に、異なるノードを要素とする3つの集合があるとし、それぞれをA、B、Cと表します。以下の2条件を満たすとき、CはAとBを分離できる構造になっています(Greenland 1999)。これを有向分離(d-separation)といいます。
- AとBを結ぶ合流点を含まないすべてのパスは、Cの要素を含んでいる
- Cに、AとBを結ぶパス上の合流点が含まれているとする。このとき、合流点を調整することでAとBを結ぶパスが生じたとしても、そのパスはCの別の要素を調整することでブロックできる
私「話がややこしくなってきた」
お父さん「そうでしょ。ノードの数が増えると、ノードの集合を考えないといけなくなって、定義が複雑になっちゃう。だから単純なケースで意味を確かめよう。この3つのDAGで、CはEとDを有向分離すると思う?」
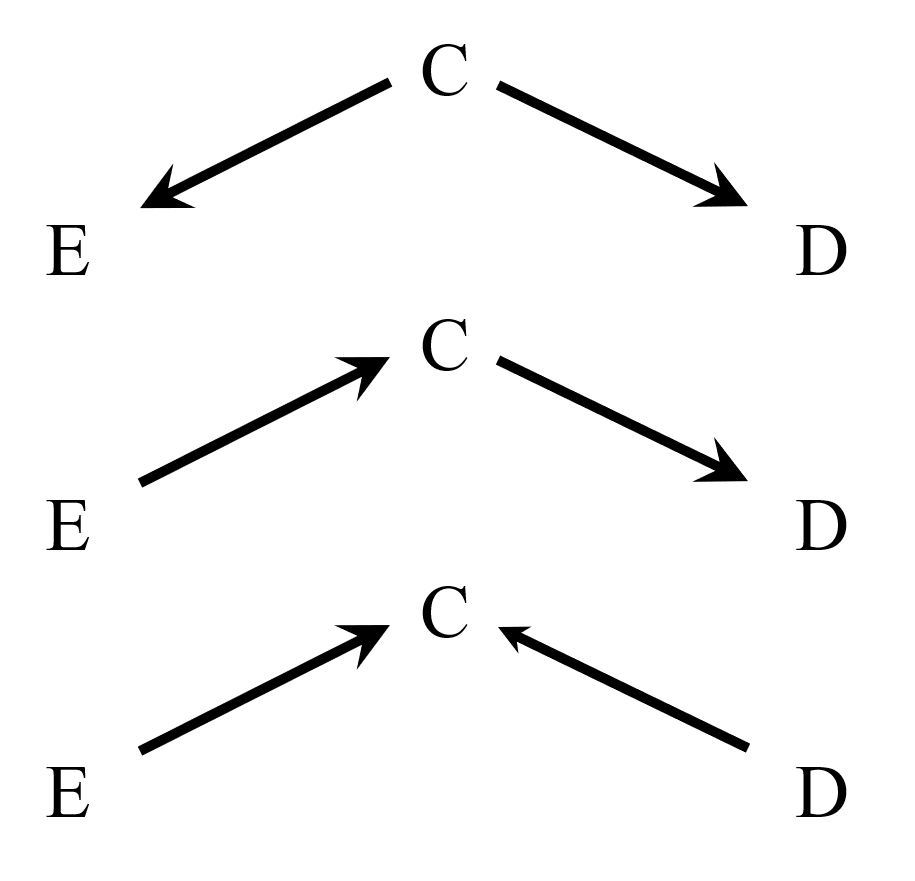
私「まず、EとDを結ぶパスはどのDAGもひとつ。上の2つのDAGは合流点を含んでいないし、パス上にCがある。だから有向分離してるはず。一番下はどうだろう。Cは合流点だし、パスE-C-Dは、別の要素で遮断できないよね。だから有向分離の条件に当てはまらない」
お父さん「その通り。共通原因や中間媒介因子で調整するとパスがブロックされるとか合流点で調整すると、パスがブロックされなくなるっていうことを正確に表現すると、上の定義になるってことがわかったでしょ。もう少しDAGが複雑になると、この定義のよさがわかると思う。このDAGで、EとDを有向分離するのは、どのノードの集合だろう」

私「合流点はないよね。だから有向分離するのはAとC?」
お父さん「それだけじゃないよね。Aだけ、またはCだけでも、有向分離の条件を満たすでしょ」
私「確かにそうね。ということは、AとCのどちらかのデータを取っておけば、交絡を調整できるってこと?」
お父さん「そういうこと。じゃあ次のDAGについて考えようか」
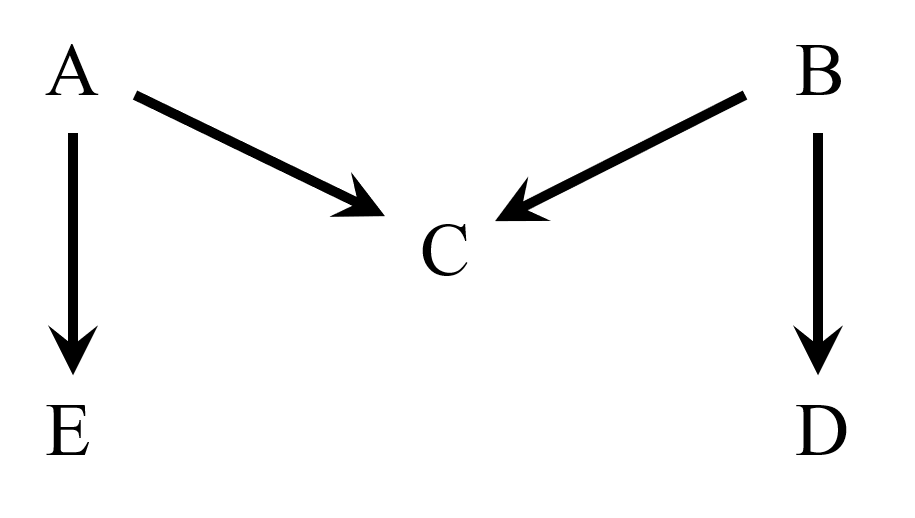
私「まだやるの?こっちから話しかけといてわるいけど、これで最後ね、お父さん。えっと、この図を考えればいいのね。AとBはそれぞれ有向分離するんじゃない?Cは合流点だから、有向分離できない」
お父さん「そこまでは正しい。だけど有向分離できるのはそれだけじゃない。AとC、またはBとCはどうだろう。Cは合流点だけど、AまたはBによってパスE←A→C←B→Dは遮断できるでしょ」
私「なるほど、二つ目の条件を使ったわけだ。丁寧に説明してくれたおかげで、有向分離がブロックの進化系っていうのは分かったつもりだけど。どういう意味があるの、これ?」
お父さん「今回の話は、ブロックをちゃんと説明するっていうのが目的だったんだけど、ぴんとこなかったかなあ。さっきのDAGについていえば、有向分離できる変数の集合を探すことで、バイアスを防げる交絡因子の組み合わせを見つけられるっていう話の流れだったんだけど」
私「ふーん。どこが分かんないのかも分からない感じになっちゃった。ひとりで考えてみる」
DAGを用いて、CがAとBを有向分離することが確認できたとします。そのとき、確率変数Cを与えた下で、AとBが条件付独立ということもわかります(Pearl 1995)。
このDAGの解釈として正しいのはどちらでしょうか。
- Cを与えた下で、EとDは条件付独立である
- Cを与えても、EとDの間には相関がある
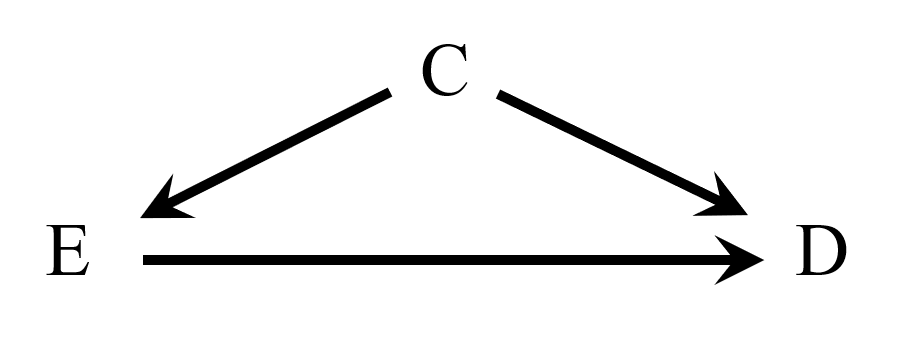
- 正解は2です。
パスE←C→DはCで遮断できますが、パスE→Dは遮断できません。したがって、CではEとDを有向分離できません。ただし、この場合には、有向分離できない理由は、EとDを結ぶ直接の因果関係が残ってしまうことであるという点に注意してください。EのDへの効果を推定するときには、(パスE→Dがあるかどうかにかかわらず)Cを調整すべきです。
このDAGの解釈として正しいのはどちらでしょうか。
- Cで条件付けないとき、EとDは独立である。また、Cを与えた下でも、EとDは条件付独立である
- Cで条件付けないとき、EとDには相関がある。一方で、Cを与えた下で、EとDは条件付独立である
- Cで条件付けないとき、EとDは独立である。一方で、Cを与えると、EとDの間には相関がある
- Cで条件付けないとき、EとDには相関がある。また、Cを与えても、EとDの間には相関がある
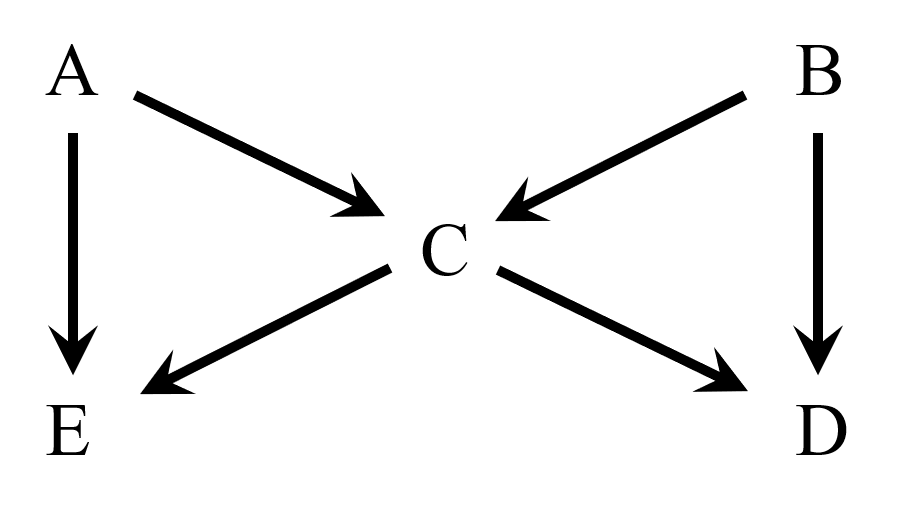
- 正解は4です。
この場合、最初のクイズとは違って、EとDを結ぶ直接のパスはありませんが、Cは合流点という問題があります。そのためCで調整すると、E←A→C←B→Dというパスが生じてしまい、やはりCでEとDを有向分離することはできません。
文献
Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology 1999;10(1):37-48
Pearl J. Causal diagrams for empirical research. Biometrika 1995; 82(4): 669-88
次のエピソード
このシリーズのエピソード
- Three-Variable DAGs: The Smallest Building Blocks of Causal Structure
- A Subtle Distinction between Common Causes and Confounders
- DAGs and Conditional Distributions: Two Languages for the Same Structure
- A Circle, an Equation, and a Cylinder
- Backdoor Paths, Block, and d-Separation: A Clue for Adjusting for Bias
- Volatility, Uncertainty, Complexity, and Ambiguity in Causal Inference
過去のシリーズ
- Study Design I
- Frequentist Thinking I
- Frequentist Experiments I
- Effects and Time I
- Adjusting for Bias I
- Truth I
用語集